题目内容
已知点A（1，-2），B（5，6），直线l经过AB的中点M，且在两坐标轴上的截距相等，则直线l的方程是 ．
考点：直线的截距式方程
专题：直线与圆
分析：求出中点坐标，当直线过原点时，求出直线方程，当直线不过原点时，设直线的方程为x+y=k，把中点坐标代入直线的方程可得k值，即得所求的直线方程．
解答：
解：点A（1，-2），B（5，6）的中点坐标公式（3，2），
当直线过原点时，方程为 y=
x，即 2x-3y=0．
当直线不过原点时，设直线的方程为x+y=k，把中点（3，2）代入直线的方程可得 k=5，
故直线方程是 x+y-5=0．
综上，所求的直线方程为 2x-3y=0，或 x+y-5=0，
故答案为：2x-3y=0，或 x+y-5=0．
当直线过原点时，方程为 y=
| 2 |
| 3 |
当直线不过原点时，设直线的方程为x+y=k，把中点（3，2）代入直线的方程可得 k=5，
故直线方程是 x+y-5=0．
综上，所求的直线方程为 2x-3y=0，或 x+y-5=0，
故答案为：2x-3y=0，或 x+y-5=0．
点评：本题考查用待定系数法求直线方程，体现了分类讨论的数学思想，注意当直线过原点时的情况，这是解题的易错点．
练习册系列答案
天天向上口算本系列答案
相关题目
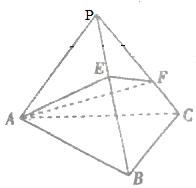如图，在三棱锥P-ABC中，三个侧面都是顶角为20°的等腰三角形，侧棱长均为a，E、F分别是PB、PC上的点，则△AEF周长的最小值为（ ）
设a＞0，b＞0，称