题目内容
在四棱锥
中,
⊥平面
，
，
,
,
,
是
的中点.
(Ⅰ)证明:⊥平面
；
(Ⅱ)若直线
与平面所成的角和与平面所成的角相等,求四棱锥的体积.
中,⊥平面，，,,,是的中点.(Ⅰ)证明:
⊥平面；(Ⅱ)若直线
与平面所成的角和与平面所成的角相等,求四棱锥的体积.(Ⅰ)略
(Ⅱ)四棱锥的体积为 
(Ⅱ)四棱锥
的体积为 (I)显然
，再证明
即可.
（2）先找出这两个线面角是解决本题的关键.过点B作
由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是
为直线PB与平面PAE
所成的角, 由
知,
为直线与平面所成的角.
从而可得
余下问题容易解决
，再证明即可.（2）先找出这两个线面角是解决本题的关键.过点B作
由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是
为直线PB与平面PAE 所成的角, 由
知,为直线与平面所成的角.从而可得
余下问题容易解决
练习册系列答案
相关题目
中，
为
的中点，则异面直线
与
所成的角为( )
中，
是正三角形，
，
. 
表示成关于
的函数；
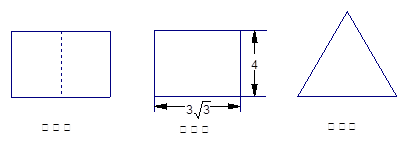
的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是_____．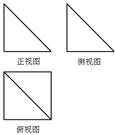
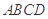的边长为2，
．将正方形
折起，
，得到三棱锥
，如图所示． 
时，求证：
；
的大小为
时，求二面角
的正切值．
