题目内容
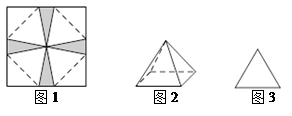
(本小题满分12分)如图，在平面四边形
中，
是正三角形，
，
.
（Ⅰ）将四边形的面积
表示成关于
的函数；
（Ⅱ）求的最大值及此时的值.
中，是正三角形，，. （Ⅰ）将四边形
的面积表示成关于的函数；（Ⅱ）求
的最大值及此时的值.（1）
；
（2）
时，
有最大值
。
；（2）
时，有最大值。本试题主要是考查了三角形面积公式的 运用，以及三角函数性质的综合运用。
（1）将所求解的四边形分解为两个三角形的面积和得到结论。
（2）根据
化为单一三角函数，然后利用值域得到最值。
解：（1）
……………………2分
………………………………4分
…………………5分
……7分
（2）
………………………9分
…………………………10分
当
时，即时，有最大值。………………………12分
（1）将所求解的四边形分解为两个三角形的面积和得到结论。
（2）根据
化为单一三角函数，然后利用值域得到最值。解：（1）
……………………2分………………………………4分…………………5分 ……7分（2）
………………………9分 …………………………10分当
时，即时，有最大值。………………………12分
练习册系列答案
快捷英语周周练系列答案
相关题目
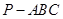中，
底面
，点
，
分别在棱
上，且
平面
；
的中点时，求
与平面
为直二面角？并说明理由.
的三个面的对角线长分别是
，则长方体对角线
的长是 
则
的形状是( )
正三角形 
等腰三角形 
直角三角形 
其他类型
中,
⊥平面
，
，
,
,
,
是
的中点.
；
与平面
．