题目内容
若函数f（x）在（0，+∞）上可导，且满足f（x）＞xf′（x），则一定有（ ）
A、函数F（x）=
| ||
B、函数F（x）=
| ||
| C、函数G（x）=xf（x）在（0，+∞）上为增函数 | ||
| D、函数G（x）=xf（x）在（0，+∞）上为减函数 |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：构造函数构造函数y=
，其导数为y'=
＜0，根据导数可知函数y=
在（0，+∞）上是减函数，问题得以解决
| f(x) |
| x |
| xf′(x)-f(x) |
| x2 |
| f(x) |
| x |
解答：
解：因为f（x）＞xf′（x），构造函数y=
，其导数为y'=
＜0，
又此知函数y=
在（0，+∞）上是减函数，
故选：B
| f(x) |
| x |
| xf′(x)-f(x) |
| x2 |
又此知函数y=
| f(x) |
| x |
故选：B
点评：本题主要考查函数的单调性与其导函数的正负情况之间的关系．属基础题．解答的关键是先得到导数的正负，再利用导数的性质得出函数的单调性．本题的难点在于构造出合适的函数．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
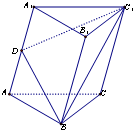如图，三棱柱ABC-A1B1C1中，D是棱AA1的中点，平面BDC1分此棱柱为上下两部分，则这上下两部分体积的比为（ ）| A、2：3 | B、1：1 |
| C、3：2 | D、3：4 |
设函数f（x）=
（a＞0，x∈R），已知区间A=[
，
]（m＜n），集合B={f（x）|m≤x≤n}，则使得A=B成立的实数a的取值范围是（ ）
| 2ax3 |
| 1+|x| |
| m2 |
| 2 |
| n2 |
| 2 |
A、a＞
| ||
B、a≤
| ||
C、0＜a≤
| ||
D、0＜a＜
|