题目内容
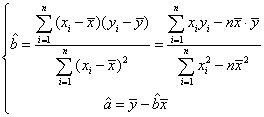 某中学有6名爱好篮球的高三男生,现在考察他们的投篮水平与打球年限的关系,每人罚篮10次,其打球年限与投中球数如下表:
某中学有6名爱好篮球的高三男生,现在考察他们的投篮水平与打球年限的关系,每人罚篮10次,其打球年限与投中球数如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 打球年限 | 3 | 5 | 6 | 7 | 9 |
| 投中球数 | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求投中球数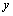 关于打球年限
关于打球年限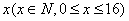 的线性回归方程,若第6名同学的打球年限为11年,试估计他的投中球数(精确到整数).
的线性回归方程,若第6名同学的打球年限为11年,试估计他的投中球数(精确到整数).
(Ⅱ)现在从高三年级大量男生中调查出打球年限超过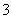 年的学生所占比例为
年的学生所占比例为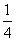 ,将上述的比例视为概率。现采用随机抽样方法在男生中每次抽取1名,抽取3次,记被抽取的3名男生中打球年限超过
,将上述的比例视为概率。现采用随机抽样方法在男生中每次抽取1名,抽取3次,记被抽取的3名男生中打球年限超过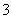 年的人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望
年的人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望 。
。
解: (Ⅰ) 设所求的线性回归方程为 ,
,
则 ,
, .
.
所以投中球数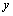 关于打球年限
关于打球年限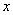 的线性回归方程为
的线性回归方程为
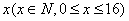 .(4分)
.(4分)
当 时,
时,

∴可以估计第6名同学投中球数为 个. (6分)
个. (6分)
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅱ)由题意可知, , (8分)
, (8分)
从而 的分布列为(要有运算过程)
的分布列为(要有运算过程)
(10分)
期望为 (12分)
(12分)

练习册系列答案
相关题目
 /个
/个


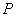



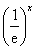 (e为自然对数的底数)成正比.当40≤x≤50时日销售量与
(e为自然对数的底数)成正比.当40≤x≤50时日销售量与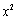 成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.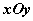 中,以原点
中,以原点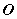 为极点,
为极点, 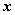 轴的正半轴为极轴建立极坐标系.若极坐标方程为
轴的正半轴为极轴建立极坐标系.若极坐标方程为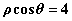 的直线与曲线
的直线与曲线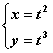 (
(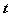 为参数)相交于
为参数)相交于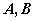 两点,则
两点,则 =( )
=( )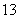 B.
B.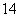 C.
C.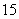 D.
D.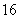
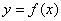 是奇函数,则
是奇函数,则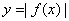 的图像关于
的图像关于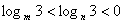 ,则
,则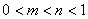 ;③若函数
;③若函数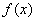 对任意
对任意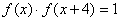 ,则8是函数
,则8是函数 中,
中,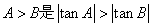 成立的充要条件;⑤命题
成立的充要条件;⑤命题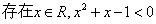 ”的否定是“
”的否定是“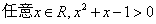 ”
”  ,那么判断框中应填入
,那么判断框中应填入 的条件是___________.
的条件是___________.
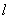 :
: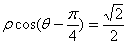 与直角坐标系中的曲线C:
与直角坐标系中的曲线C: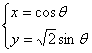 (
(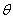 为参数),
为参数),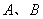 两点.
两点.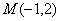 与
与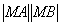 .
.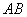 是半圆
是半圆 的直径,
的直径, 是弧
是弧 是线段
是线段 ,则
,则 的值是 ( )
的值是 ( ) B.
B.  C.
C.  D.
D.

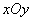 中,以坐标原点为极点,以
中,以坐标原点为极点,以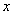 轴的非负半轴为极轴,建立极坐标系,已知直线
轴的非负半轴为极轴,建立极坐标系,已知直线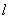 的参数方程为
的参数方程为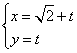 (t为参数),圆
(t为参数),圆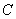 的极坐标方程是
的极坐标方程是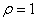 。
。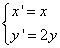 得到曲线
得到曲线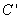 ,设
,设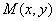 为曲线
为曲线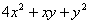 的最大值,并求相应点
的最大值,并求相应点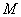 的坐标.
的坐标. =3+i求复数z.
=3+i求复数z.