题目内容
16．如果实数x，y满足约束条件$\left\{\begin{array}{l}{x+2y-4≥0}\\{x-y+2≥0}\\{2x+y-3≤0}\end{array}\right.$，则2x-y的最小值为（ ）| A． | -2 | B． | -$\frac{5}{3}$ | C． | -$\frac{1}{3}$ | D． | 1 |
分析 画出约束条件的可行域，判断目标函数经过的位置，求解目标函数的最小值即可．
解答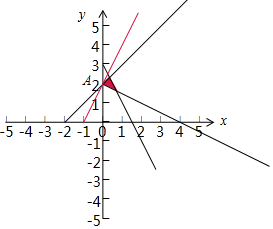 
解：根据约束条件$\left\{\begin{array}{l}{x+2y-4≥0}\\{x-y+2≥0}\\{2x+y-3≤0}\end{array}\right.$画出可行域如图，
令z=2x-y，
可得y=2x-z，当直线y=2x-z经过A时取得最小值．
由：$\left\{\begin{array}{l}{x+2y-4=0}\\{x-y+2=0}\end{array}\right.$，
可得A（0，2），当直线过点（0，2）时，
2x-y取最小值-2．
故选：A．
点评 本题考查线性规划的简单应用，画出可行域是解题的关键之一，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
6．已知集合U={x|x＞0}，∁UA={x|0＜x＜3}，那么集合A=（ ）
| A． | {x|x＞3} | B． | {x|x≥3} | C． | {x|x＜0或x＞3} | D． | {x|x≤0或x≥3} |
1．已知函数f（x）=sin2x+$\sqrt{3}$（1-2sin2x）．
（Ⅰ）求f（x）的单调减区间；
（Ⅱ）当x∈[-$\frac{π}{6}$，$\frac{π}{6}$]时，求f（x）的值域．
（Ⅰ）求f（x）的单调减区间；
（Ⅱ）当x∈[-$\frac{π}{6}$，$\frac{π}{6}$]时，求f（x）的值域．
5．O为坐标原点，F为抛物线C：y=$\frac{1}{4}$x2的焦点，P为C上一点，若|PF|=3，则△POF的面积为（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | 1 |
6．f（x）是R上的偶函数，当x≤0时，f（x）=x3+ln（x+1），当x＞0时，f（x）（ ）
| A． | -x3-ln（1-x） | B． | x3+ln（1-x） | C． | x3-ln（1-x） | D． | -x3+ln（1-x） |