题目内容
6.f(x)是R上的偶函数,当x≤0时,f(x)=x3+ln(x+1),当x>0时,f(x)( )| A. | -x3-ln(1-x) | B. | x3+ln(1-x) | C. | x3-ln(1-x) | D. | -x3+ln(1-x) |
分析 利用函数的奇偶性与已知条件转化求解即可.
解答 解:f(x)是R上的偶函数,可得f(-x)=f(x);
当x≤0时,f(x)=x3+ln(x+1),
则当x>0时,f(x)=f(-x)=-x3+ln(1-x).
故选:D.
点评 本题考查函数的奇偶性的应用,函数的解析式的求法,是基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
16.如果实数x,y满足约束条件$\left\{\begin{array}{l}{x+2y-4≥0}\\{x-y+2≥0}\\{2x+y-3≤0}\end{array}\right.$,则2x-y的最小值为( )
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
14.下列选项中,说法正确的是( )
| A. | 命题“?x0∈R,${x_0}^2-{x_0}≤0$”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则$sinA>\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
11.已知{an}为等差数列,其前n项和为Sn,若S9=12,则下列各式一定为定值的是( )
| A. | a3+a8 | B. | a10 | C. | a3+a5+a7 | D. | a2+a7 |
18.给出下列四个函数,在(0,+∞)为增函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=(x-1)2 | C. | y=2-x | D. | y=log2(x+2) |
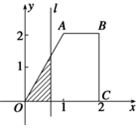 如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )
如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )