题目内容
7.已知函数f(x)=2cos2$\frac{x}{2}$-2$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$-1,x∈R.(I)求使得取f(x)得最大值的x的取值集合;
(II)若g(x)=x+f(x),求g(x)的单调递减区间.
分析 (I)化简函数f(x),求出f(x)得最大值的x的取值集合;
(II)求函数g(x)的导数,利用函数单调性和导数之间的关系解g(x)的单调递减区间.
解答 解:( I)∵$f(x)=cosx-\sqrt{3}sinx=2cos(x+\frac{π}{3})$,
当$x+\frac{π}{3}=2kπ$,即$x=2kπ-\frac{π}{3}$时,f(x)取得最大值2.
所以使得f(x)取得最大值的x的取值集合为$\{x|x=2kπ-\frac{π}{3},k∈Z\}$.
( II)∵$g(x)=x+cosx-\sqrt{3}sinx$,
∴$g'(x)=1-sinx-\sqrt{3}cosx$.
令g'(x)<0,得$1-sinx-\sqrt{3}cosx<0$,
∴$sinx+\sqrt{3}cosx>1$,
∴$2sin(x+\frac{π}{3})>1$,
∴$sin(x+\frac{π}{3})>\frac{1}{2}$,
∴$2kπ+\frac{π}{6}<x+\frac{π}{3}<kπ+\frac{5π}{6}$,k∈Z,
∴$2kπ-\frac{π}{6}<x<2kπ+\frac{π}{2}$,k∈Z,
∴g(x)的单调递减区间为$[2kπ-\frac{π}{6},2kπ+\frac{π}{2}]$,k∈Z.
点评 本题主要考查函数单调性和单调区间的求解,利用正弦函数的单调性的性质或者导数法时解决本题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
17.已知a,b,c均为直线,α,β为平面,下面关于直线与平面关系的命题:
①任意给定一条直线与一个平面α,则平面α内必存在与a垂直的直线;
②a∥β,β内必存在与a相交的直线;
③α∥β,a?α,b?β,必存在与a,b都垂直的直线;
其中正确命题的个数为( )
①任意给定一条直线与一个平面α,则平面α内必存在与a垂直的直线;
②a∥β,β内必存在与a相交的直线;
③α∥β,a?α,b?β,必存在与a,b都垂直的直线;
其中正确命题的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.如果a>b>0,那么下列不等式成立的是( )
| A. | -a>-b | B. | a+c>b+c | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | (-a)2>(-b)2 |
16.如果实数x,y满足约束条件$\left\{\begin{array}{l}{x+2y-4≥0}\\{x-y+2≥0}\\{2x+y-3≤0}\end{array}\right.$,则2x-y的最小值为( )
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
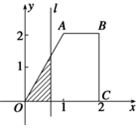 如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )
如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )