题目内容
5.O为坐标原点,F为抛物线C:y=$\frac{1}{4}$x2的焦点,P为C上一点,若|PF|=3,则△POF的面积为( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 1 |
分析 根据抛物线方程求得抛物线的准线方程与焦点坐标,利用|PF|=4,求得P点的纵坐标,代入抛物线方程求得横坐标,代入三角形面积公式计算即可得到.
解答 解:由抛物线方程得准线方程为:y=-1,焦点F(0,1),
又P为C上一点,|PF|=3,
可得yP=2,
代入抛物线方程得:|xP|=2$\sqrt{2}$,
∴S△POF=$\frac{1}{2}$|OF|•|xP|=$\sqrt{2}$.
故选:B.
点评 本题考查了抛物线的定义及几何性质,熟练掌握抛物线上的点所满足的条件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果实数x,y满足约束条件$\left\{\begin{array}{l}{x+2y-4≥0}\\{x-y+2≥0}\\{2x+y-3≤0}\end{array}\right.$,则2x-y的最小值为( )
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
20.复数z=(2-i)(1+2i)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.根据如下样本数据
得到的回归直线方程为$\hat y=bx+a$.若样本中心为(5,0.9),则x每减少1个单位,y就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | a+b-4 | -0.5 | 0.5 | -2 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加1.2个单位 | D. | 减少1.2个单位 |
14.下列选项中,说法正确的是( )
| A. | 命题“?x0∈R,${x_0}^2-{x_0}≤0$”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则$sinA>\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
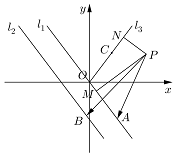 如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
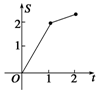
如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;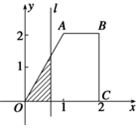 如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )
如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )