题目内容
8.已知双曲线M:$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e=$\frac{{2\sqrt{3}}}{3}$,且S△ABF=1-$\frac{{\sqrt{3}}}{2}$.抛物线N的顶点在坐标原点,焦点为F.(1)求双曲线M和抛物线N的方程;
(2)设动直线l与抛物线N相切于点P,与抛物线的准线相交于点Q,则以PQ为直径的圆是否恒过y轴上的一个定点?如果经过,试求出该点的坐标,如果不经过,试说明理由.
分析 (1)根据双曲线的离心率公式及三角形的面积公式,即可求得a和b的值,即可求得双曲线的方程,求得焦点坐标,即可求得p的值,求得抛物线N的方程;
(2)利用导数求得切线方程,联立y=-2,即可求得Q点坐标,根据向量数量积的坐标,由$\frac{2-m}{8}$x02+m(m+2)-8=0,对任意实数x0(x0≠0)恒成立,即可求得m的值,即可求得以PQ为直径的圆是否恒过y轴上的一个定点.
解答 解:(1)由双曲线M:$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1(a>0,b>0)的离心率e=$\frac{c}{a}$=$\frac{{2\sqrt{3}}}{3}$,①
三角形的面积S=$\frac{1}{2}$(c-a)b=1-$\frac{\sqrt{3}}{2}$,②
由c2=a2+b2,③
解得:a=$\sqrt{3}$,b=1,c=2,
∴双曲线的标准方程:$\frac{{y}^{2}}{3}-{x}^{2}=1$,则双曲线的上焦点F(0,2),
则抛物线N的方程:x2=8y;
(2)由(1)可得抛物线N的方程:x2=8y,准线方程y=-2,
由y=$\frac{1}{8}$x2,y′=$\frac{1}{4}$x,设P(x0,$\frac{1}{8}$x02),则直线l的方程y-$\frac{1}{8}$x02=$\frac{1}{4}$x0(x-x0),
即y=$\frac{1}{4}$x0x-$\frac{1}{8}$x02,联立y=-2,则Q($\frac{{x}_{0}^{2}-16}{2{x}_{0}}$,-2),
假设存在定点M(0,m)满足假设条件,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$=0,对任意点恒成立,
则$\overrightarrow{MP}$=(x0,$\frac{1}{8}$x02-m),$\overrightarrow{MQ}$=($\frac{{x}_{0}^{2}-16}{2{x}_{0}}$,-2-m),
∴$\frac{{x}_{0}^{2}-16}{2}$-(m+2)($\frac{1}{8}$x02-m)=0,即$\frac{2-m}{8}$x02+m(m+2)-8=0,对任意实数x0(x0≠0)恒成立,
$\left\{\begin{array}{l}{2-m=0}\\{m(m+2)-8=0}\end{array}\right.$,解得:m=2,
∴以PQ为直径的圆经过y轴上的定点M(0,2).
点评 本题考查双曲线的简单几何性质,直线与双曲线的位置关系,考查抛物线的性质,向量数量积的坐标运算,考查计算能力,属于中档题.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案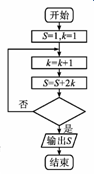 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )| A. | k>5? | B. | k>4? | C. | k>7? | D. | k>6? |
| A. | x2+y2=16 | B. | x2+y2=16(x≥4) | C. | x2-y2=16 | D. | x2-y2=16(x≥4) |
| A. | 4n | B. | 4n+1 | C. | 4n+2 | D. | 4n+3 |
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
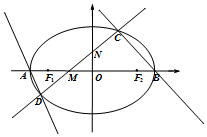 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,