题目内容
19.已知方程cos2x+$\sqrt{3}$sin2x=k+1.(1)k为何值时,方程在区间[0,$\frac{π}{2}$]内有两个相异的解α,β;
(2)当方程在区间[0,$\frac{π}{2}$]内有两个相异的解α,β时,求α+β的值.
分析 (1)令f(x)=cos2x+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$),根据函数图象判断k的范围;
(2)求出f(x)在[0,$\frac{π}{2}$]上的对称轴,根据图象的对称性得出α+β的值.
解答 解:(1)令f(x)=cos2x+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$),
作出f(x)在[0,$\frac{π}{2}$]上的函数图象如图所示: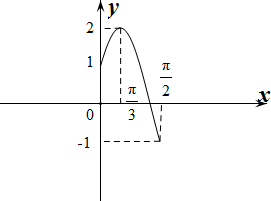
由图象可知当1≤k+1<2即0≤k<1时,f(x)=k+1有两个相异的解.
(2)令2x+$\frac{π}{6}$=$\frac{π}{2}$+kπ,解得x=$\frac{π}{3}$+$\frac{kπ}{2}$,
∴f(x)在[0,$\frac{π}{2}$上的对称轴为x=$\frac{π}{3}$,
∴α+β=$\frac{2π}{3}$.
点评 本题考查了三角函数的恒等变换,正弦函数的图象与性质,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
14.函数y=sin(x+$\frac{π}{6}$)的一个递减区间是( )
| A. | [-$\frac{π}{2}$,$\frac{π}{2}$] | B. | [-π,0] | C. | [-$\frac{2π}{3}$,$\frac{2π}{3}$] | D. | [$\frac{π}{3}$,$\frac{4π}{3}$] |
4.定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈[0,1)}\\{-{(\frac{1}{2})}^{|x-\frac{3}{2}|},x∈[1,2)}\end{array}\right.$,若x∈[-4,2)时,f(x)≥$\frac{t}{4}$-$\frac{1}{2t}$恒成立,则实数t的取值范围是( )
| A. | [-2,0)∪(0,1) | B. | [-2,0)∪[1,+∞) | C. | [-2,1] | D. | (-∞,-2]∪(0,1] |
8.a,b是两条异面直线,A是不在a,b上的点,则下列结论成立的是( )
| A. | 过A且平行于a和b的平面可能不存在 | |
| B. | 过A有且只有一个平面平行于a和b | |
| C. | 过A至少有一个平面平行于a和b | |
| D. | 过A有无数个平面平行于a和b |