题目内容
4.定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈[0,1)}\\{-{(\frac{1}{2})}^{|x-\frac{3}{2}|},x∈[1,2)}\end{array}\right.$,若x∈[-4,2)时,f(x)≥$\frac{t}{4}$-$\frac{1}{2t}$恒成立,则实数t的取值范围是( )| A. | [-2,0)∪(0,1) | B. | [-2,0)∪[1,+∞) | C. | [-2,1] | D. | (-∞,-2]∪(0,1] |
分析 令-4≤x<-2,则0≤x+4<2,由f(x+2)=2f(x),求出f(x)=$\frac{1}{4}$f(x+4),画出y=f(x)和y=$\frac{1}{4}$f(x+4)的图象,求出最小值,将x∈[-4,2)时,f(x)≥$\frac{t}{4}$-$\frac{1}{2t}$恒成立,转化为x∈[-4,2),f(x)min≥$\frac{t}{4}$-$\frac{1}{2t}$,解出不等式即可求出实数t的取值范围.
解答 解:令-4≤x<-2,则0≤x+4<2,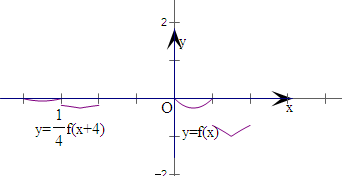
∵f(x+2)=2f(x),
∴f(x+4)=2f(x+2)=4f(x),
即f(x)=$\frac{1}{4}$f(x+4),
画出y=f(x)和y=$\frac{1}{4}$f(x+4)的图象,
当x=1.5时,f(x+4)取最小值-1,
由x∈[-4,2),f(x)≥$\frac{t}{4}$-$\frac{1}{2t}$恒成立,
则-$\frac{1}{4}$≥$\frac{t}{4}$-$\frac{1}{2t}$,解得t≤-2或0<t≤1.
故选:D.
点评 本题考查分段函数的图象及应用,考查函数的最值及运用,考查不等式恒成立问题转化为求最值,考查数形结合的能力,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
13.若直线l与平面α内的一条直线平行,则l和α的位置关系是( )
| A. | l?α | B. | l∥α | C. | l?α或l∥α | D. | l和α相交 |