题目内容
已知函数f(x)=loga(x2-4x+8),x∈[0,2]的最大值为-2,则a= .
考点:复合函数的单调性
专题:函数的性质及应用
分析:根据复合函数单调性之间的关系以及对数函数的性质进行求解即可.
解答:
解:设t=x2-4x+8=(x-2)2+4,则函数等价为g(t)=logat,
当x∈[0,2],则t∈[4,8],
若a>1,则函数的最大值为g(8)=loga8=-2,此时不成立,
若0<a<1,则函数的最大值为g(4)=loga4=-2,即a-2=
=4,
解得a=
,
故答案为:
.
当x∈[0,2],则t∈[4,8],
若a>1,则函数的最大值为g(8)=loga8=-2,此时不成立,
若0<a<1,则函数的最大值为g(4)=loga4=-2,即a-2=
| 1 |
| a2 |
解得a=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查函数最值的求解,根据复合函数单调性之间的关系以及对数函数的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的值域是( )
| 2x |
| 2x+1 |
| A、(0,1) |
| B、(0,1] |
| C、(0,+∞) |
| D、[0,+∞) |
设P、Q是函数f(x)=2sin(2x+φ)(φ为常数)图象上的两点且横坐标分别为-
、
,若f(x)图象上存在一个最高点M,使得(
+
)•
=0,则下列关系一定成立的是 ( )
| π |
| 12 |
| π |
| 4 |
| MP |
| MQ |
| PQ |
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(-
|
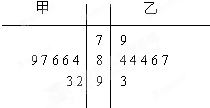 如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.