题目内容
3.下列命题正确的是①③.(写出所有正确命题的序号)①已知a,b∈R,“a>1且b>1”是“ab>1”的充分条件;
②已知平面向量$\overrightarrow a,\overrightarrow b$,“$|\overrightarrow a|>1$且$|\overrightarrow b|>1$”是“$|\overrightarrow a+\overrightarrow b|>1$”的必要不充分条件;
③已知a,b∈R,“a2+b2≥1”是“|a|+|b|≥1”的充分不必要条件;
④命题P:“?x0∈R,使${e^{x_0}}≥{x_0}+1$且lnx0≤x0-1”的否定为¬p:“?x∈R,都有ex<x+1且lnx>x-1”
分析 ①,由不等式的性质判定;
②,利用向量的加法法则判定;
③,利用单位圆判定;
④,“且”的否定是“或”
解答 解;对于①,已知a,b∈R,“a>1且b>1”是“ab>1”的充分条件,正确;
对于②,向量的加法法则可知,“$|\overrightarrow a|>1$且$|\overrightarrow b|>1$”不能得到“$|\overrightarrow a+\overrightarrow b|>1$”;“$|\overrightarrow a+\overrightarrow b|>1$”,不能得到,“$|\overrightarrow a|>1$且$|\overrightarrow b|>1$”,故错;
对于③,如图在单位圆x2+y2=1上或圆外任取一点P(a,b),满足“a2+b2≥1”,根据三角形两边之和大于第三边,一定有“|a|+|b|≥1”,在单位圆内任取一点M(a,b),满足“|a|+|b|≥1”,但不满足,“a2+b2≥1”,故正确;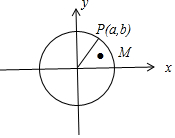
对于④,命题P:“?x0∈R,使${e^{x_0}}≥{x_0}+1$且lnx0≤x0-1”的否定为¬p:“?x∈R,都有ex<x+1或lnx>x-1”,故错.
故答案为:①③
点评 本题考查了命题真假的判定,涉及到充要条件、命题的四种形式等基础知识,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
14.z=$\frac{5i}{1-2i}$(i是虚数单位),则z为( )
| A. | 2-i | B. | 2+i | C. | -2-i | D. | -2+i |
15.设a,b∈R,则“a+b>4”是“a>1且b>3”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
17.已知全集U={1,3,5,7,9},集合A={1,5},B={3,5},则∁UA∩∁UB=( )
| A. | {7,9} | B. | {1,3,7,9} | C. | {5} | D. | {1,3,5} |
