题目内容
20.在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,q=$\frac{{S}_{2}}{{b}_{2}}$.(1)求an与bn;
(2)若对于?n∈N*,不等式$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$<t恒成立,求实数t的取值范围.
分析 (1)通过设等差数列{an}的公差为d,联立b2+S2=12及q=$\frac{{S}_{2}}{{b}_{2}}$,计算即得公差和公比,进而可得结论;
(2)通过(1)裂项可知$\frac{1}{{S}_{n}}$=$\frac{2}{3}$($\frac{1}{n}$-$\frac{1}{n+1}$),进而利用并项相消法计算、放缩即得结论.
解答 解:(1)设等差数列{an}的公差为d,
∵b2+S2=12,q=$\frac{{S}_{2}}{{b}_{2}}$,
∴q+6+d=12、q=$\frac{6+d}{q}$,
解得:q=3或q=-4(舍),d=3,
∴an=3+3(n-1)=3n,bn=3n-1;
(2)由(1)可知$\frac{1}{{S}_{n}}$=$\frac{2}{n(3+3n)}$=$\frac{2}{3}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$=$\frac{2}{3}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=$\frac{2}{3}$(1-$\frac{1}{n+1}$),
∵n≥1,
∴$\frac{2}{3}$(1-$\frac{1}{n+1}$)<$\frac{2}{3}$,
∴t≥$\frac{2}{3}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,利用裂项相消法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
8.已知a,b∈R,且ab≠0,那么“a>b”是“lg(a-b)>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.“?n∈N*,a${\;}_{n+1}^{2}$=anan+2”是“数列{an}为等比数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
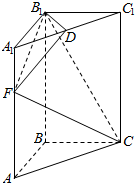 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.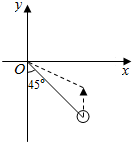 如图,据气象部门预报,在距离码头O南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动,距台风中心450km以内的地区都将受到影响.据以上预报估计,从现在起多长时间后,该码头将受到热带风暴的影响,影响时间大约有多长?(精确到0.1h,$\sqrt{2}≈$1.414)
如图,据气象部门预报,在距离码头O南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动,距台风中心450km以内的地区都将受到影响.据以上预报估计,从现在起多长时间后,该码头将受到热带风暴的影响,影响时间大约有多长?(精确到0.1h,$\sqrt{2}≈$1.414)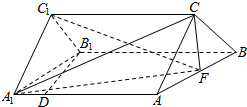 已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.
已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.