题目内容
11．如果函数f（x）=x2-ax-3在区间（-∞，3]上单调递减，则实数a满足的条件使（ ）| A． | a≤6 | B． | a≥6 | C． | a≥3 | D． | a≥-3 |
分析 根据函数f（x）=x2-ax-3在区间（-∞，3]上单调递减，则根据函数的图象知：对称轴必在x=3的右边，列出不等式求解即可．
解答 解：∵f（x）=x2-ax-3在区间（-∞，3]上递减，对称轴为x=$\frac{a}{2}$，
∴$\frac{a}{2}$≥3，
故a≥6，
故选：B．
点评 本题考查了二次函数的性质，二次函数的对称轴的求法与应用，属于基础题．
练习册系列答案
相关题目
1．已知函数f（x）的导函数f′（x）=（1-x）e-x．若f（x）在（m，m+2）上单调递增，则实数m的取值范围是（ ）
| A． | [1，+∞） | B． | （-∞，1] | C． | [-1，+∞） | D． | （-∞，-1] |
19．
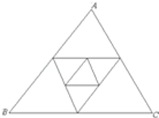如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（ ）
如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（ ）| A． | $\frac{1}{2002}$ | B． | $\frac{1}{2001}$ | C． | $\frac{1}{{2}^{2002}}$ | D． | 2${\;}^{\frac{1}{2001}}$ |
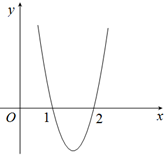已知函数f（x）=2x3+bx2+cx，其导函数y=f′（x）的图象（如图所示）经过点（1，0），（2，0）．