题目内容
如图，已知AB⊥AC，AB=3，AC=
，圆A是以A为圆心半径为1的圆，圆B是以B为圆心的圆．设点P，Q分别为圆A，圆B上的动点，且
=
，则
•
的取值范围是 ．
| 3 |
| AP |
| 1 |
| 2 |
| BQ |
| CP |
| CQ |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设∠QBA=θ，则∠PAC=90°+θ，从而有
=
-
，
=
-
，通过计算求出即可．
| CP |
| AP |
| AC |
| CQ |
| BQ |
| BC |
解答：
解：设∠QBA=θ，则∠PAC=90°+θ，
∵
=
-
，
=
-
∴
•
=（
-
）（
-
）
=
•
-
•
-
•
+
•
=2-0-
cos（90°+θ）+3
=5+
sinθ，
∵-1≤sinθ≤1，
∴
•
∈[5-
，5+
]．
∵
| CP |
| AP |
| AC |
| CQ |
| BQ |
| BC |
∴
| CP |
| CQ |
| AP |
| AC |
| BQ |
| BC |
=
| AP |
| BQ |
| AP |
| BC |
| AC |
| BQ |
| AC |
| BC |
=2-0-
| 3 |
=5+
| 3 |
∵-1≤sinθ≤1，
∴
| CP |
| CQ |
| 3 |
| 3 |
点评：本题考查了平面向量的数量积的运算，是一道基础题．
练习册系列答案
相关题目
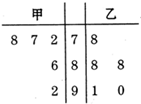甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别是. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|