题目内容
设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,f(x)=(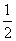 )x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为________.
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为________.
( ,2)
,2)
[解析]

依题意得,f(x+4)=f(x),即函数f(x)是以4为周期的函数.关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,等价于函数f(x)与g(x)=loga(x+2)(a>1)的图象恰有三个不同的交点.结合题意分别画出函数f(x)在(-2,6]上的图象与函数g(x)=loga(x+2)(a>1)的图象(如图所示),结合图象分析可知,要使两函数的图象有三个不同的交点,则有 由此解得
由此解得 <a<2,即a的取值范围是(
<a<2,即a的取值范围是( ,2).
,2).

练习册系列答案
相关题目
已知函数f(x)的图象是连续不断的,有如下的x、f(x)对应值表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 123.56 | 21.45 | -7.82 | 11.57 | -53.76 | -126.49 |
函数f(x)在区间[1,6]上的零点有( )
A.2个 B.3个
C.至多2个 D.至少3个
 的值为 ( )
的值为 ( )
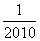 -
-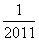 -
-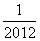 -
-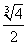 B.
B.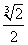
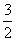
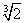 D.不确定
D.不确定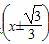 2+y2=
2+y2=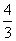 B.
B. 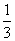
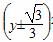 2=
2=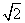 时,求直线l的方程.
时,求直线l的方程. 中,
中, ,则
,则 的值是 。
的值是 。