题目内容
定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4]时,f(x)=x2-2x,则函数f(x)在[0,2013]上的零点个数是________.
604
[解析] 由f(x)+f(x+5)=16,可知f(x-5)+f(x)=16,则f(x+5)-f(x-5)=0,所以f(x)是以10为周期的周期函数.∵x∈(-1,4]时,x2∈[0,16],2x∈(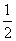 ,16],∴x2-2x<16,∴x∈(-1,4]时,f(x)<16.
,16],∴x2-2x<16,∴x∈(-1,4]时,f(x)<16.
∴当x∈(4,9]时,x-5∈(-1,4],∴f(x-5)<16,
f(x)=16-f(x+5)=16-f(x-5)>0,∴f(x)在(4,9]上无零点,因此在一个周期(-1,9]上,函数f(x)=x2-2x在区间(-1,4]内有3个零点,在(4,9]区间内无零点,故f(x)在一个周期内仅有3个零点,由于区间(3,2013]中包含201个周期,且在区间[0,3]内也存在一个零点x=2,故f(x)在[0,2013]上的零点个数为3×201+1=604.

练习册系列答案
相关题目
 ,2)在幂函数f(x)的图象上,点(-2,
,2)在幂函数f(x)的图象上,点(-2,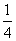 )在幂函数g(x)的图象上,当x分别为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x)成立?
)在幂函数g(x)的图象上,当x分别为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x)成立?
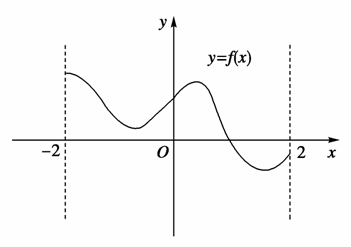
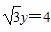 相切.
相切. ·
·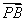 的取值范围.
的取值范围.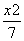 -
-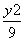 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上,且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上,且|AK|=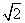 |AF|,则△AFK的面积为( )
|AF|,则△AFK的面积为( )