题目内容
2.若二次函数y=x2+tx+t+3的函数值恒大于0,则实数t的取值范围是[-2,6].分析 根据二次函数的性质的判别式小于0,解出关于t的不等式即可.
解答 解:由题意得:
△=t2-4(t+3)<0,
解得:-2<t<6,
故答案为:[-2,6].
点评 本题考查了二次函数的性质,考查根的判别式问题,是一道基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
11.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}\end{array}\right.$,则z=3x-y的取值范围为( )
| A. | [0,$\frac{12}{5}$] | B. | [0,2] | C. | [2,$\frac{12}{5}$] | D. | [2,$\frac{8}{3}$] |
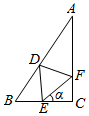 △ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.
△ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.