题目内容
已知x2+y2=5,则x+2y的取值范围为 .
考点:基本不等式
专题:三角函数的求值,不等式的解法及应用
分析:由x2+y2=5,令x=
cosθ,y=
sinθ,θ∈[0,2π).则x+2y=5sin(θ+φ),其中φ=arctan2.利用正弦函数的单调性即可得出.
| 5 |
| 5 |
解答:
解:由x2+y2=5,令x=
cosθ,y=
sinθ,θ∈[0,2π).
则x+2y=
cosθ+2
sinθ=5sin(θ+φ),其中φ=arctan2.
∵-1≤sin(θ+φ)≤1,
∴x+2y的取值范围为[-5,5].
故答案为:[-5,5].
| 5 |
| 5 |
则x+2y=
| 5 |
| 5 |
∵-1≤sin(θ+φ)≤1,
∴x+2y的取值范围为[-5,5].
故答案为:[-5,5].
点评:本题考查了圆的参数方程、三角函数代换、正弦函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A、y=sinx | ||
| B、y=2x | ||
| C、y=x3-x | ||
D、y=lg(x+
|
已知{an}的前n项和Sn=n2-6n,则当n≥4时,|a1|+|a2|+…+|an|的值是( )
| A、n2-6n-18 | ||
B、
| ||
| C、n2-6n+18 | ||
D、
|
已知集合A={cos0,sin270°},B={x|x+1=0},那么A∩B( )
| A、{0,1} | B、{1,-1} |
| C、{1} | D、{-1} |
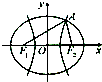 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-