题目内容
已知数列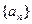 ,
,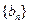 满足
满足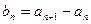 ,其中
,其中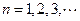 .
.
(Ⅰ)若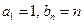 ,求数列
,求数列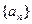 的通项公式;
的通项公式;
(Ⅱ)若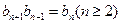 ,且
,且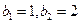 .
.
(ⅰ)记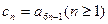 ,求证:数列
,求证:数列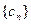 为等差数列;
为等差数列;
(ⅱ)若数列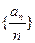 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项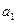 应满足的条件.
应满足的条件.
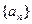 ,
,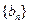 满足
满足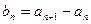 ,其中
,其中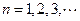 .
.(Ⅰ)若
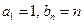 ,求数列
,求数列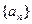 的通项公式;
的通项公式;(Ⅱ)若
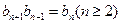 ,且
,且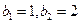 .
.(ⅰ)记
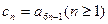 ,求证:数列
,求证:数列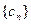 为等差数列;
为等差数列;(ⅱ)若数列
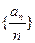 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项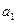 应满足的条件.
应满足的条件.(Ⅰ)
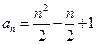
(Ⅱ)
(ⅰ)证明略
(ⅱ)设集合

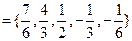 ,
,当
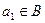 时,数列
时,数列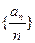 中必有某数重复出现无数次.
中必有某数重复出现无数次.当
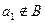 时,
时,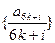
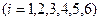 均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列
均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列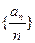 中任意一项的值均未在该数列中重复出现无数次
中任意一项的值均未在该数列中重复出现无数次解:(Ⅰ)当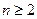 时,有
时,有
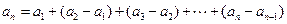
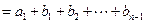 …………2分
…………2分
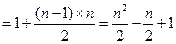 . ………………3分
. ………………3分
又因为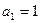 也满足上式,所以数列
也满足上式,所以数列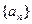 的通项为
的通项为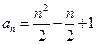 .…………4分
.…………4分
(Ⅱ)(ⅰ)因为对任意的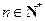 有
有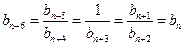 ,………………5分
,………………5分
所以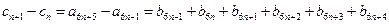
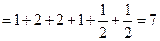
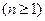 ,
,
所以数列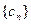 为等差数列. ………………7分
为等差数列. ………………7分
(ⅱ)设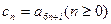 ,(其中
,(其中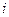 为常数且
为常数且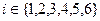 ),所以
),所以
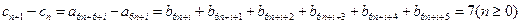
所以数列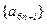 均为以7为公差的等差数列. ………………9分
均为以7为公差的等差数列. ………………9分
设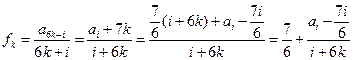 ,
,
(其中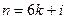
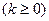 ,
,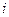 为
为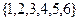 中的一个常数),
中的一个常数),
当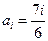 时,对任意的
时,对任意的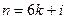 有
有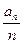
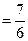 ; ………………10分
; ………………10分
当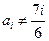 时,
时,
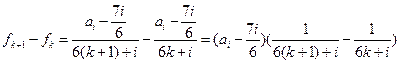
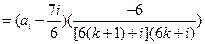 ……………11分
……………11分
①若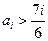 ,则对任意的
,则对任意的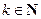 有
有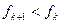 ,所以数列
,所以数列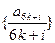 为单调减数列;
为单调减数列;
②若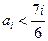 ,则对任意的
,则对任意的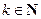 有
有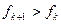 ,所以数列
,所以数列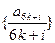 为单调增数列;…12分
为单调增数列;…12分
综上:设集合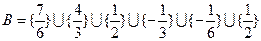
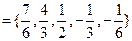 ,
,
当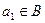 时,数列
时,数列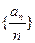 中必有某数重复出现无数次.
中必有某数重复出现无数次.
当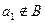 时,
时,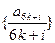
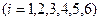 均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列
均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列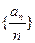 中任意一项的值均未在该数列中重复出现无数次. ……14分
中任意一项的值均未在该数列中重复出现无数次. ……14分
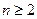 时,有
时,有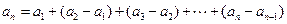
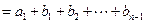 …………2分
…………2分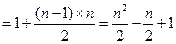 . ………………3分
. ………………3分又因为
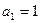 也满足上式,所以数列
也满足上式,所以数列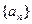 的通项为
的通项为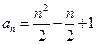 .…………4分
.…………4分(Ⅱ)(ⅰ)因为对任意的
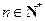 有
有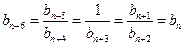 ,………………5分
,………………5分所以
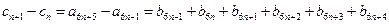
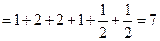
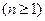 ,
,所以数列
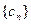 为等差数列. ………………7分
为等差数列. ………………7分(ⅱ)设
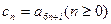 ,(其中
,(其中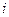 为常数且
为常数且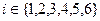 ),所以
),所以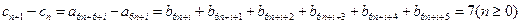
所以数列
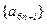 均为以7为公差的等差数列. ………………9分
均为以7为公差的等差数列. ………………9分设
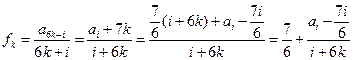 ,
,(其中
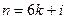
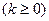 ,
,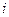 为
为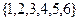 中的一个常数),
中的一个常数),当
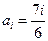 时,对任意的
时,对任意的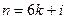 有
有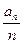
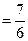 ; ………………10分
; ………………10分当
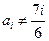 时,
时,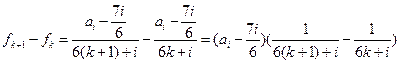
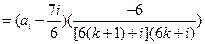 ……………11分
……………11分①若
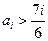 ,则对任意的
,则对任意的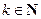 有
有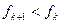 ,所以数列
,所以数列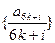 为单调减数列;
为单调减数列;②若
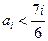 ,则对任意的
,则对任意的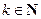 有
有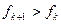 ,所以数列
,所以数列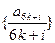 为单调增数列;…12分
为单调增数列;…12分综上:设集合
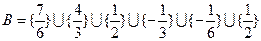
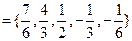 ,
,当
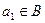 时,数列
时,数列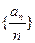 中必有某数重复出现无数次.
中必有某数重复出现无数次.当
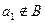 时,
时,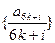
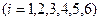 均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列
均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列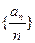 中任意一项的值均未在该数列中重复出现无数次. ……14分
中任意一项的值均未在该数列中重复出现无数次. ……14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
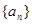 是等差数列,且
是等差数列,且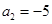 ,
,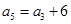 ,则
,则
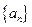 的前
的前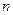 项和为
项和为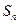 ,满足
,满足
 满足
满足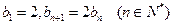 ,
,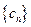 满足
满足 ,数列
,数列 项和为
项和为 ,求
,求 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的 的值是否可以等于2011?为此,他设计了一个程序
的值是否可以等于2011?为此,他设计了一个程序 (如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
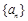 为等比数列,且
为等比数列,且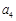 是
是 与
与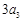 的等差中项,若
的等差中项,若 ,则该数列的前5项的和为 ( )
,则该数列的前5项的和为 ( )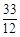

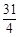
 满足
满足 ,
, .
.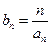 ,求数列
,求数列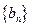 的前
的前 项和
项和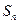
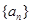 的通项公式
的通项公式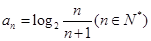 ,设其前n项和为
,设其前n项和为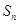 ,则使
,则使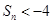 成立的自然
成立的自然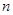 有 ( )
有 ( )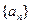 ,
,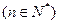 是等差数列,则有数列
是等差数列,则有数列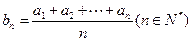 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列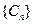 是等比数列,且
是等比数列,且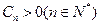 ,则有
,则有 _____ _____
_____ _____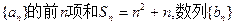 满足
满足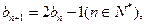 且
且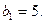
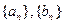 的通项公式;
的通项公式;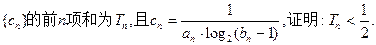
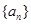 是等差数列,
是等差数列,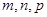 是互不相等的正整数,有正确的结论:
是互不相等的正整数,有正确的结论: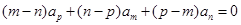 ,类比上述性质,相应地,若等比数列
,类比上述性质,相应地,若等比数列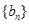 ,
,