题目内容
7.有一个综艺节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐,选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,某机构随机抽取50个参与节目的选手的年龄作为样本进行分析研究,由此得到如下频数分布表(所有参与节目的选手年龄都在[5,65)内).| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 2 | 12 | 16 | 10 | 7 | 3 |
(Ⅱ)若将频率视为概率,从参与节目的选手中随机抽取3位(看作有放回地抽取),求年龄在[35,45)内的选手人数X的分布列、数学期望.
分析 (Ⅰ)由已知作出频率分布表,从而能画出频率分布直方图.
(Ⅱ)50个选手中年龄在[35,45)内的选手人数为:10人,将频率视为概率,从参与节目的选手中随机抽取3位(看作有放回地抽取),年龄在[35,45)内的选手人数X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出年龄在[35,45)内的选手人数X的分布列、数学期望.
解答 解:(Ⅰ)由已知作出频率分布表:
| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 2 | 12 | 16 | 10 | 7 | 3 |
| 频率 | 0.04 | 0.24 | 0.32 | 0.2 | 0.14 | 0.06 |

(Ⅱ)50个选手中年龄在[35,45)内的选手人数为:10人,
将频率视为概率,从参与节目的选手中随机抽取3位(看作有放回地抽取),年龄在[35,45)内的选手人数X的可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{40}^{3}}{{C}_{50}^{3}}$=$\frac{247}{490}$,
P(X=1)=$\frac{{C}_{10}^{1}{C}_{40}^{2}}{{C}_{50}^{3}}$=$\frac{195}{490}$,
P(X=2)=$\frac{{C}_{10}^{2}{C}_{40}^{1}}{{C}_{50}^{3}}$=$\frac{45}{490}$,
P(X=3)=$\frac{{C}_{10}^{3}}{{C}_{50}^{3}}$=$\frac{3}{490}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{247}{490}$ | $\frac{195}{490}$ | $\frac{45}{490}$ | $\frac{3}{490}$ |
点评 本题考查频率分布直方图的画法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.角-330°的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知sin4$\frac{x}{4}$+cos4$\frac{x}{4}$=1,在sin(2016π+x)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 0 | C. | -$\frac{\sqrt{2}}{2}$ | D. | -1 |
16.在△ABC中,角A,B,C对应的边分别为a,b,c,若b-acosB=acosC-c,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
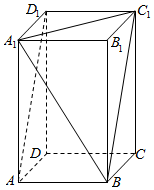 在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$
在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$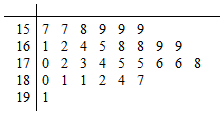 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”