题目内容
已知数列{an}中,a1=1,a2=2,a3=3,且对n∈N+,an•an+1•an+2•an+3=24,则其前2013项和S2013= .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知,an•an+1•an+2•an+3=24,以n+1代n,得出an+1•an+2•an+3•an+4=24,两式相除可推断出an+4=an,进而可知数列{an}是以4为周期的数列,只要看2013是4的多少倍,然后a1=1,a2=2,a3=3,求出a4,而2013是4的503倍余1,故可知S2013=503×(1+2+3+4)+1答案可得.
解答:
解:依题意可知,an•an+1•an+2•an+3=24,以n+1代n,得出an+1•an+2•an+3•an+4=24,
两式相除可推断出an+4=an,
∴数列{an}是以4为周期的数列,
求得a4=4.
∴S2013=503×(1+2+3+4)+1=5031
故答案为:5031.
两式相除可推断出an+4=an,
∴数列{an}是以4为周期的数列,
求得a4=4.
∴S2013=503×(1+2+3+4)+1=5031
故答案为:5031.
点评:本题主要考查了数列的递推式和数列的求和问题.本题的关键是找出数列的周期性,是中档题.

练习册系列答案
相关题目
已知 tanα>0,cosα<0,则角α的终边在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
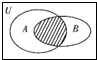 设全集U=R,A={x∈Z|-2≤x≤2},B={x∈R|x2+3x<0},则如图中阴影部分表示的集合为( )
设全集U=R,A={x∈Z|-2≤x≤2},B={x∈R|x2+3x<0},则如图中阴影部分表示的集合为( )| A、{-1} |
| B、{-2,-1} |
| C、{-2,-1,0} |
| D、(-2,-1) |