Question

7．函数f（x）=|lnx|-$\frac{1}{8}$x²的图象大致为（　　）

• A．
• B．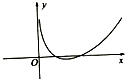
• C．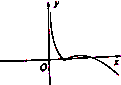
• D．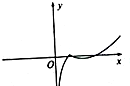

Answer 1

分析 根据函数的定义域，极限，单调性判断．

解答 解：f（x）的定义域为{x|x＞0}，排除A．
当x→0⁺时，f（x）→+∞，排除D．
当x＞1时，f（x）=lnx-$\frac{{x}^{2}}{8}$，f′（x）=$\frac{1}{x}-\frac{x}{4}$，
令f′（x）=0解得x=2，
当x＞2时，f′（x）＜0，
∴f（x）在（2，+∞）上是减函数，排除B．
故选C．

点评 本题考查了函数图象的判断，通常从函数的单调性，特殊点等方面采用排除法判断．