题目内容
2．抛物线的顶点在原点，对称轴为y轴，抛物线上一点（x0，2）到焦点的距离为3，则抛物线方程为x2=4y．分析 利用抛物线的性质，判断抛物线的方程的形状，求出p即可得到抛物线方程．
解答 解：抛物线的顶点在原点，对称轴为y轴，抛物线上一点（x0，2），
可知抛物线方程为：x2=2py，抛物线上一点（x0，2）到焦点的距离为3，
可得$\frac{p}{2}$=1，解得p=2，所求的抛物线方程为：x2=4y．
故答案为：x2=4y．
点评 本题考查抛物线的简单性质的应用，抛物线方程的求法，考查计算能力．
练习册系列答案
相关题目
12．已知数列{an}满足a1=1，an+1=an2+an，设bn=$\frac{1}{{a}_{n}+1}$，用[x]表示不超过x的最大整数，则[b1+b2+…+b8]的值为（ ）
| A． | 1 | B． | 0 | C． | 2 | D． | 8 |
随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．
10．已知命题p：“?x0∈R，e${\;}^{{x}_{0}}$-x0-1≤0”，则￢p为（ ）
| A． | ?x0∈R，e${\;}^{{x}_{0}}$-x0-1≥0 | B． | ?x0∈R，e${\;}^{{x}_{0}}$-x0-1＞0 | ||
| C． | ?x∈R，ex-x-1＞0 | D． | ?x∈R，ex-x-1≥0 |
17．复数（$\frac{1-ai}{a+i}$）2017=（ ）
| A． | 1 | B． | -1 | C． | i | D． | -i |
7．设全集U=R，集合A={x|x≥2}，B={x|0≤x＜6}，则集合（∁UA）∩B=（ ）
| A． | {x|0＜x＜2} | B． | {x|0＜x≤2} | C． | {x|0≤x＜2} | D． | {x|0≤x≤2} |
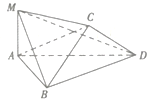如图，将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD丄平面CBD，若AM丄平面ABD，且AM=$\sqrt{2}$
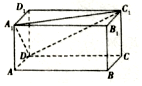在长方体ABCD-A1B1C1D1中，AB=4，AD=2，AA1=2，点E在棱AB上移动．
12．已知集合A={x|y=$\sqrt{x+1}$}，B={y=|y=1-ex}，则A∩B=（ ）
| A． | [-1，1） | B． | [-1，1] | C． | （-1，1） | D． | （-∞，-1]∪[1，+∞） |