题目内容
12.已知数列{an}满足a1=1,an+1=an2+an,设bn=$\frac{1}{{a}_{n}+1}$,用[x]表示不超过x的最大整数,则[b1+b2+…+b8]的值为( )| A. | 1 | B. | 0 | C. | 2 | D. | 8 |
分析 数列{an}是增数列,且 an+1=an2+an=an(1+an),得到$\frac{1}{{a}_{n+1}}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n}+1}$,从而 b1+b2+…+b8=$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}+…+\frac{1}{{a}_{8}+1}$=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{9}}$<$\frac{1}{{a}_{1}}$=1,由此能求出[b1+b2+…+b8]
解答 解:∵数列{an}满足:a1=1,an+1=an2+an,
∴an+1-an=an2>0,
∴数列{an}是增数列,且 $\frac{1}{{a}_{n}}$>0,
∵an+1=an2+an=an(1+an),
∴$\frac{1}{{a}_{n+1}}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n}+1}$,从而 b1+b2+…+b8=$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}+…+\frac{1}{{a}_{8}+1}$=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{9}}$<$\frac{1}{{a}_{1}}$=1,
a1=1,a2=2,a3=6,>1,
∴b1+b2+…+b8∈(0,1),
∴[b1+b2+…+b8]=0.
故选:B.
点评 本题考查等差数列的前n项和的求法及应用,是中档题,解题时要注意裂项求和法的合理运用.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
3.已知f(x)=ln(e2x+1)+xcos2x,则f($\frac{π}{3}$)-f(-$\frac{π}{3}$)=( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
20.已知函数f(x)=x(m+e-x),其中e为自然对数的底数,曲线y=f(x)上存在不同的两点,使得曲线在这两点处的切线都与y轴垂直,则实数m的取值范围是( )
| A. | (0,e-2) | B. | (e-2,+∞) | C. | (0,e2) | D. | (e2,+∞) |
7.下列变量中不属于分类变量的是( )
| A. | 性别 | B. | 吸烟 | C. | 宗教信仰 | D. | 国籍 |
1.设A,B是非空集合,定义A*B={x|x∈A∪B且x∉A∩B},已知M={x|0≤x≤3},N={y|y≤1},则M*N=( )
| A. | (1,3] | B. | (-∞,0)∪(1,3] | C. | (-∞,3] | D. | (-∞,0]∪[1,3] |
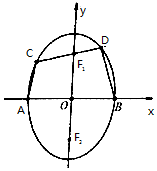 已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.
已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.