题目内容
11.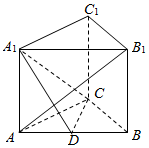 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.(Ⅰ)证明:CD⊥平面AA1B1B;
(Ⅱ)AA1=1,AC=2,求三棱锥C1-A1DC的体积.
分析 (1)由AA1⊥平面ABC得AA1⊥CD,由AB1⊥平面A1CD得AB1⊥CD,故CD⊥平面AA1B1B;
(2)由CD⊥平面AA1B1B得CD⊥AB,得出△ABC是等腰直角三角形,以△A1C1C为棱锥的底面,则D到平面A1C1CA的距离h=$\frac{1}{2}BC$=$\frac{1}{2}AC=1$.代入棱锥的体积公式计算.
解答 解:(I)∵AA1⊥平面ABC,CD?平面ABC,
∴AA1⊥CD,
∵AB1⊥平面A1CD,CD?A1CD,
∴AB1⊥CD.
又AA1?平面AA1B1B,AB1?平面AA1B1B,AA1∩AB1=A,
∴CD⊥平面AA1B1B.
(II)∵CD⊥平面AA1B1B,AB?平面AA1B1B,
∴CD⊥AB,
又∵D是AB的中点,
∴△ABC是等腰三角形,BC=AC=2.
∵AA1⊥平面ABC,BC?平面ABC,
∴AA1⊥BC,
又∵AC⊥BC,AA1?平面AA1C1C,AC?平面AA1C1C,AA1∩AC=A,
∴BC⊥平面AA1C1C,
∵D是AB的中点,
∴D到平面AA1C1C的距离h=$\frac{1}{2}BC$=1.
∵S${\;}_{△{A}_{1}{C}_{1}C}$=$\frac{1}{2}{A}_{1}{C}_{1}•A{A}_{1}$=$\frac{1}{2}×2×1$=1,
∴V${\;}_{{C}_{1}-{A}_{1}DC}$=V${\;}_{D-{A}_{1}{C}_{1}C}$=$\frac{1}{3}{S}_{△{A}_{1}{C}_{1}C}•h$=$\frac{1}{3}×1×1=\frac{1}{3}$.
点评 本题考查了线面垂直的性质与判定,棱锥的体积计算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.根据我国发布的《环境空气质量指数(AQI)技术规定》:空气质量指数划分为0~50、51~100、101~150、151~200、201~300和大于300六级,对应于空气质量指数的六个级别,指数越大,级别越高,说明污染越,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于150时,可以户外运动;空气质量指数151及以上,不适合进行旅游等户外活动.以下是济南市2015年12月中旬的空气质量指数情况:
(I)求12月中旬市民不适合进行户外活动的概率;
(Ⅱ)一外地游客在12月来济南旅游,想连续游玩两天,求适合旅游的概率.
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(Ⅱ)一外地游客在12月来济南旅游,想连续游玩两天,求适合旅游的概率.
6.为了对某课题进行研究,用分层抽样的方法从三所高校A,B,C的相关人中抽取若干人组成研究小组,有关数据如下表(单位:人).
(1)求x,y;
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
| 高校 | 相关人数 | 抽取人数 |
| A | 54 | x |
| B | 36 | 2 |
| C | 72 | y |
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
3.某洗衣机生产流水线上有三条不同的作业线,每条作业线上的质量指标分别为x,y,z,用综合指标S=x+y+z评价该洗衣机的等级.若S≥5,则该洗衣机为特等品;若4≤S≤5,则该洗衣机为一等品;若S<4,则该洗衣机不合格.现从这一批洗衣机中,随机抽取10台作为样本,其质量指标列表如下:
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)从编号为A1到A6的6台洗衣机中,随机抽取2台,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2台洗衣机中,恰有一台是一等品一台不合格”,求事件B发生的概率.
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)从编号为A1到A6的6台洗衣机中,随机抽取2台,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2台洗衣机中,恰有一台是一等品一台不合格”,求事件B发生的概率.
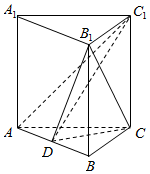 如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.
如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.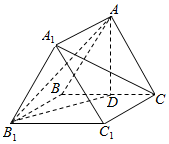 如图,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.
如图,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.