题目内容
已知a和b是任意非零实数．
（1）求证
≥4；
（2）若不等式|a+b|+|a-b|≥|a（|2+x|+|2-x|）恒成立，求实数x的取值范围．
（1）求证
| |2a+b|+|2a-b| |
| |a| |
（2）若不等式|a+b|+|a-b|≥|a（|2+x|+|2-x|）恒成立，求实数x的取值范围．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（1）利用绝对值三角不等式，可证得
=|2+
|+|2-
|≥|（2+
）+（2-
）|=4；
（2）利用绝对值三角不等式
≥
=2，于是可得|2+x|+|2-x|≤2，解之即可．
| |2a+b|+|2a-b| |
| |a| |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
（2）利用绝对值三角不等式
| |a+b|+|a-b| |
| |a| |
| |a+b+a-b| |
| |a| |
解答：
（1）证明：
=|
|+|
|=|2+
|+|2-
|≥|（2+
）+（2-
）|=4；
（2）解：由|a+b|+|a-b|≥|a|（|2+x|+|2-x|）恒成立，得
≥（|2+x|+|2-x|）恒成立，
又因为
≥
=2，
所以，|2+x|+|2-x|≤2，
又|2+x|+|2-x|≥|（2+x）+（2-x）|=4，
∴|2+x|+|2-x|≤2的解集为∅．
| |2a+b|+|2a-b| |
| |a| |
| 2a+b |
| a |
| 2a-b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
（2）解：由|a+b|+|a-b|≥|a|（|2+x|+|2-x|）恒成立，得
| |a+b|+|a-b| |
| |a| |
又因为
| |a+b|+|a-b| |
| |a| |
| |a+b+a-b| |
| |a| |
所以，|2+x|+|2-x|≤2，
又|2+x|+|2-x|≥|（2+x）+（2-x）|=4，
∴|2+x|+|2-x|≤2的解集为∅．
点评：本题考查绝对值三角不等式的解法，着重考查等价转化思想与运算求解能力，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
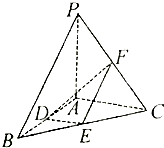如图，在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=90°，D、E、F分别是棱AB、BC、CP的中点，AB=AC=1，PA=2．
我国政府对PM2.5采用如下标准：