题目内容
已知数列{an}中,a1=1,an+1=
,求证:数列{a2n-
}是等比数列.
|
| 3 |
| 2 |
考点:数列递推式,等比关系的确定
专题:等差数列与等比数列
分析:根据数列的递推关系,结合等比数列的定义将条件进行转化即可得到结论.
解答:
解:令n=1时,a2=
a1+1=
+1=
,
则a2n=
a2n-1+2n-1=
[a2n-2-3(2n-2)]+2n-1=
a2n-2+1,
则a2n-
=
a2n-2+1-
=
a2n-2-
=
(a2n-2-
),
则
=
,
故数列{a2n-
}是公比q=
的等比数列.
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
则a2n=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
则a2n-
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
则
a2n-
| ||
a2n-2-
|
| 1 |
| 3 |
故数列{a2n-
| 3 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查递推数列的应用,以及等比数列的证明,根据等比数列的定义是解决本题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、12+π | B、8+π |
| C、12-π | D、6-π |
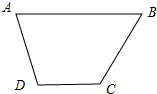 如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )
如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )