题目内容
已知tanα=-
，则
=（ ）
| 1 |
| 2 |
| 1+2sinαcosα |
| sin2α-cos2α |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式利用同角三角函数间基本关系变形后，将tanα的值代入计算即可求出值．
解答：
解：∵tanα=-
，
∴原式=
=
=
=-
．
故选：C．
| 1 |
| 2 |
∴原式=
| sin2α+2sinαcosα+cos2α |
| sin2α-cos2α |
| tan2α+2tanα+1 |
| tan2α-1 |
| ||
|
| 1 |
| 3 |
故选：C．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
已知离散型随机变量X等可能取值1，2，3，…，n若P（1≤X≤3）=
，则n的值为（ ）
| 1 |
| 5 |
| A、3 | B、5 | C、10 | D、15 |
若点P（cosα，sinα）在直线y=-2x上，则sinα•cosα=（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
△ABC中，已知b=30，c=15，角C=30°，则此三角形的解的情况是（ ）
| A、一解 | B、二解 |
| C、无解 | D、无法确定 |
下列表述正确的是（ ）
①归纳推理是由特殊到一般的推理；
②演绎推理是由一般到特殊的推理；
③类比推理是由特殊到一般的推理；
④分析法是一种间接证明法；
⑤若z∈C，且|z+2-2i|=1，则|z-2-2i|的最小值是3．
①归纳推理是由特殊到一般的推理；
②演绎推理是由一般到特殊的推理；
③类比推理是由特殊到一般的推理；
④分析法是一种间接证明法；
⑤若z∈C，且|z+2-2i|=1，则|z-2-2i|的最小值是3．
| A、①②③④ | B、②③④ |
| C、①②④⑤ | D、①②⑤ |
设数列{an}是单调递增的等差数列，前三项的和为12，前三项的积为48，则a1=（ ）
| A、1 | B、2 | C、±2 | D、4 |
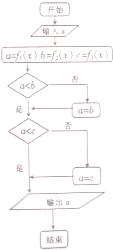已知函数f1（x）=x，f2（x）=