题目内容
5.$\lim_{n→∞}\frac{{n•{3^n}}}{{n{{(x-2)}^n}+n•{3^{n+1}}-{3^n}}}=\frac{1}{3}$则实数x的取值范围是( )| A. | [-1,5] | B. | (-1,5) | C. | [-1,5] | D. | (-5,5) |
分析 对原式分子分母同除以n•3n,可得$\underset{lim}{n→∞}$$\frac{1}{n}$=0,$\underset{lim}{n→∞}$($\frac{x-2}{3}$)n=0,解不等式|$\frac{x-2}{3}$|<1,即可得到所求范围.
解答 解:$\lim_{n→∞}\frac{{n•{3^n}}}{{n{{(x-2)}^n}+n•{3^{n+1}}-{3^n}}}=\frac{1}{3}$,即为
$\underset{lim}{n→∞}$$\frac{1}{(\frac{x-2}{3})^{n}+3-\frac{1}{n}}$=$\frac{1}{3}$,
即有$\underset{lim}{n→∞}$$\frac{1}{n}$=0,$\underset{lim}{n→∞}$($\frac{x-2}{3}$)n=0,
即为|$\frac{x-2}{3}$|<1,解得-1<x<5.
故选:B.
点评 本题考查数列的极限的求法,注意常见数列的极限,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.若log4[log3(1og2x)]=0,则x${\;}^{-\frac{1}{2}}$等于( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 8 | D. | 4 |
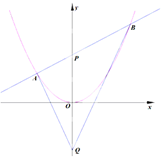 如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.
如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.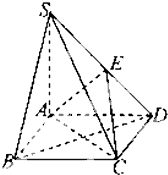 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.