题目内容
20.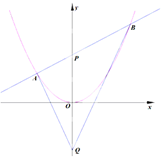 如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.
如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.(Ⅰ) 求证:x1x2=-4m;
(Ⅱ) 若$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,且$\overrightarrow{QP}$⊥($\overrightarrow{QA}$-μ$\overrightarrow{QB}$),求证:λ=μ.
分析 (Ⅰ)设出直线l的方程,得到方程组,表示出x1•x2即可;(Ⅱ)由$\overrightarrow{QP}$⊥($\overrightarrow{QA}$-μ$\overrightarrow{QB}$),表示出关于λ,μ的方程,解出即可.
解答 解:(Ⅰ)设l方程为:y=kx+m,由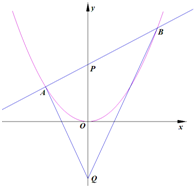
$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}=4y}\end{array}\right.$得:x2-4kx-4m=0,
所以x1•x2=-4m;
(Ⅱ) $\overrightarrow{AP}$=λ$\overrightarrow{PB}$,得$\frac{{x}_{1}}{{x}_{2}}$=λ,
由$\overrightarrow{QP}$⊥($\overrightarrow{QA}$-μ$\overrightarrow{QB}$),
得2m[y1-μy2+(1-μ)m]=0,
从而$\frac{{{x}_{1}}^{2}}{4}$-μ$\frac{{{x}_{2}}^{2}}{4}$+(1-μ)m=0,
把x1•x2=-4m;
代入上式得${(\frac{{x}_{1}}{{x}_{2}})}^{2}$-(1-μ)$\frac{{x}_{1}}{{x}_{2}}$-μ=0,
则λ2+(1-μ)λ-μ=0,
所以λ=-1或λ=μ,而显然λ>0,
所以λ=μ.
点评 本题考查了抛物线问题,考查向量的垂直的性质,考查转化思想,是一道中档题.

练习册系列答案
相关题目
8.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+a2-1=0垂直,则a=( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | 1 | D. | -2 |
15.设M={1,2,3,4,5,6,7,8,9,10},由M到M上的一一映射中,有7个数字和自身对应的映射个数是( )
| A. | 120 | B. | 240 | C. | 107 | D. | 360 |
5.$\lim_{n→∞}\frac{{n•{3^n}}}{{n{{(x-2)}^n}+n•{3^{n+1}}-{3^n}}}=\frac{1}{3}$则实数x的取值范围是( )
| A. | [-1,5] | B. | (-1,5) | C. | [-1,5] | D. | (-5,5) |