题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2) 减函数,证明见解析;(3)
(2) 减函数,证明见解析;(3) ![]() .
.
【解析】
(1)利用奇函数的性质令![]() ,求解
,求解![]() 即可.
即可.
(2)利用函数的单调性的定义证明即可.
(3)利用函数是奇函数以及函数的单调性转化不等式为代数形式的不等式,求解即可.
(1)∵![]() 在定义域
在定义域![]() 上是奇函数,
上是奇函数,
所以![]() ,即
,即![]() ,∴
,∴![]() ,
,
经检验,当![]() 时,原函数是奇函数.
时,原函数是奇函数.
(2)![]() 在
在![]() 上是减函数,证明如下:
上是减函数,证明如下:
由(1)知![]() ,
,
任取![]() ,设
,设![]() ,
,
则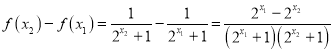 ,
,
∵函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() ,
,
∴函数![]() 在
在![]() 上是减函数.
上是减函数.
(3)因![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于![]() ,
,
由(2)知![]() 在
在![]() 上是减函数,由上式推得
上是减函数,由上式推得![]() ,
,
即对任意![]() ,有
,有![]() 恒成立,
恒成立,
由 ,
,
令![]() ,
,![]() ,则可设
,则可设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:℃),对某种鸡的时段产蛋量
(单位:℃),对某种鸡的时段产蛋量![]() (单位:
(单位: ![]() )和时段投入成本
)和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根据散点图判断, ![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为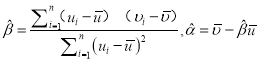
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |