题目内容
下列函数中,值域是(0,+∞)的是 ( )A.y=31-x
B.y=
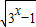
C.y=7
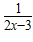
D.y=log2(x-3)
【答案】分析:根据一次函数及反比例函数的图象和性质,求出y=1-x以及y=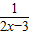 的值域,再根据指数函数的性质判断A和C是否正确;根据指数函数的性质,求出3x-1≥0的值域,再由幂函数的性质判断B是否正确;根据一次函数的图象和性质,求出y=x-3的值域,再由对数函数的性质可判断D是否正确
的值域,再根据指数函数的性质判断A和C是否正确;根据指数函数的性质,求出3x-1≥0的值域,再由幂函数的性质判断B是否正确;根据一次函数的图象和性质,求出y=x-3的值域,再由对数函数的性质可判断D是否正确
解答:解:A、设y=1-x,则此函数的值域是R,故函数y=31-x的值域是(0,+∞),故A正确;
B、由y=3x-1≥0得,函数y=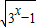 的值域是[0,+∞),故B不正确;
的值域是[0,+∞),故B不正确;
C、由y=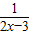 ≠0得,函数y=7
≠0得,函数y=7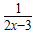 的值域是(0,1)∪(1,+∞),故C不正确;
的值域是(0,1)∪(1,+∞),故C不正确;
D、因y=x-3>0,故函数y=log2(x-3)的值域是R,故D不正确.
故选A.
点评:本题的考点是复合函数的值域,对于指数型的函数先求出指数的范围,再根据指数函数的性质求值域;对于幂函数型的应先求底数的范围,再根据幂函数的性质求值域.
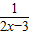 的值域,再根据指数函数的性质判断A和C是否正确;根据指数函数的性质,求出3x-1≥0的值域,再由幂函数的性质判断B是否正确;根据一次函数的图象和性质,求出y=x-3的值域,再由对数函数的性质可判断D是否正确
的值域,再根据指数函数的性质判断A和C是否正确;根据指数函数的性质,求出3x-1≥0的值域,再由幂函数的性质判断B是否正确;根据一次函数的图象和性质,求出y=x-3的值域,再由对数函数的性质可判断D是否正确解答:解:A、设y=1-x,则此函数的值域是R,故函数y=31-x的值域是(0,+∞),故A正确;
B、由y=3x-1≥0得,函数y=
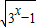 的值域是[0,+∞),故B不正确;
的值域是[0,+∞),故B不正确;C、由y=
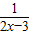 ≠0得,函数y=7
≠0得,函数y=7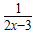 的值域是(0,1)∪(1,+∞),故C不正确;
的值域是(0,1)∪(1,+∞),故C不正确;D、因y=x-3>0,故函数y=log2(x-3)的值域是R,故D不正确.
故选A.
点评:本题的考点是复合函数的值域,对于指数型的函数先求出指数的范围,再根据指数函数的性质求值域;对于幂函数型的应先求底数的范围,再根据幂函数的性质求值域.

练习册系列答案
相关题目
下列函数中,值域是[-2,2]的是( )
| A、f(x)=2x-1 | ||
| B、f(x)=log0.5(x+11) | ||
C、f(x)=
| ||
| D、f(x)=x2(4-x2) |
下列函数中,值域是(0,+∞)的函数是( )
A、y=x-
| ||
| B、y=x2+x+1 | ||
C、y=
| ||
| D、y=|log2(x+1)| |