题目内容
12.已知集合A={1,2,3,4},B={x|x=2n,n∈A },则A∩B=( )| A. | { 1,4} | B. | { 2,4} | C. | { 9,16} | D. | {2,3} |
分析 把A中元素代入x=2n中计算求出x的值,确定出B,找出A与B的交集即可.
解答 解:把x=1,2,3,4分别代入x=2n得:x=2,4,6,8,即B={2,4,6,8},
∵A={1,2,3,4},
∴A∩B={2,4},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
3.函数f(x)=1-ex的图象与x轴相交于点P,则曲线在点P处的切线的方程为( )
| A. | y=-e•x+1 | B. | y=-x+1 | C. | y=-x | D. | y=-e•x |
7.已知四棱锥P-ABCD的底面为菱形,∠BAD=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法中错误的是( )
| A. | 异面直线PA与BC的夹角为60° | B. | 若M为AD的中点,则AD⊥平面PMB | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
4.已知集合A={1,2,3,4},B={x|y=2x,y∈A},则A∩B=( )
| A. | {2} | B. | {1,2} | C. | {2,4} | D. | {1,2,4} |
1.设F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使得$(\overrightarrow{OP}+\overrightarrow{O{F_2}})•\overrightarrow{{F_2}P}=0$,其中O为坐标原点,且$|\overrightarrow{P{F_1}}|=3|\overrightarrow{P{F_2}}|$,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{5}{2}$ |
2.集合A={x||x-1|<2},B={x|$\frac{1}{9}$<3x<9},则A∩B=( )
| A. | (-1,3) | B. | (-1,2) | C. | (-2,2) | D. | (-2,3) |
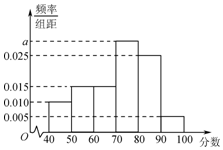 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),