题目内容
9.已知命题p:方程x2-2mx+7m-10=0无解,命题q:x∈(0,+∞),x2-mx+4≥0恒成立,若p∨q是真命题,且p∧q也是真命题,求m的取值范围.分析 由p∨q是真命题,且p∧q也是真命题得:p与q两个都是真命题,然后求解p,q为真时参数m的范围求解交集,可得答案.
解答 解:当命题p为真时,有:△=(-2m)2-4(7m-10)<0,
解得:2<m<5;
当命题q为真时,有:m≤$\frac{{x}^{2}+4}{x}$=x+$\frac{4}{x}$,对x∈(0,+∞)恒成立,
即m≤(x+$\frac{4}{x}$)min,
而x∈(0,+∞)时,(x+$\frac{4}{x}$)min=4,当x=2时取等号.
即m≤4,
由p∨q是真命题,且p∧q也是真命题得:p与q都是真命题;
即2<m≤4,
综上,所求m的取值范围是(2,4].
点评 本题以命题的真假判断与应用为载体,考查了复合命题,方程根的个数判断,函数恒成立等知识点,难度中档.

练习册系列答案
相关题目
4.一圆的面积以10πcm2/s速度增加,那么当圆半径r=20cm时,其半径r的增加速率u为( )
| A. | $\frac{1}{2}$cm/s | B. | $\frac{1}{3}$cm/s | C. | $\frac{1}{4}$cm/s | D. | $\frac{1}{5}$cm/s |
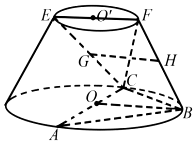 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.