题目内容
7.抛物线y2=2x的焦点到准线的距离为1.分析 利用抛物线的标准方程可得 p=1,由焦点到准线的距离为p,从而得到结果.
解答 解:抛物线y2=2x的焦点到准线的距离为p,由标准方程可得p=1,
故答案是:1.
点评 本题考查抛物线的标准方程,以及简单性质的应用,判断焦点到准线的距离为p是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15.在四边形 ABCD 中,若$\overrightarrow{AB}$=-$\frac{1}{2}$$\overrightarrow{CD}$,则此四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 梯形 | D. | 矩形 |
2.已知数列{an}的前n项和Sn=n2-2n-1,则a1+a17=( )
| A. | 31 | B. | 29 | C. | 30 | D. | 398 |
2.已知x∈(0,+∞)时,不等式9x-m•3x+m+1>0恒成立,则m的取值范围是( )
| A. | 2-2$\sqrt{2}$<m<2+2$\sqrt{2}$ | B. | m<2 | C. | m<2+2$\sqrt{2}$ | D. | m$≥2+2\sqrt{2}$ |
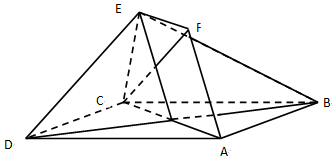 (文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF. 四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.
四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.