题目内容
6.已知f(x)=x5-2x4+x3+x2-x-5,应用秦九韶算法计算x=5的值是2015.分析 利用秦九韶算法计算多项式的值,先将多项式转化为f(x)=x5-2x4+x3+x2-x-5=((((x-2)x+1)x+1)x-2)x-5的形式,然后求解即可.
解答 解:f(x)=x5-2x4+x3+x2-x-5=((((x-2)x+1)x+1)x-2)x-5
则f(5)=((((5-2)5+1)5+1)5-2)5-5
=2015.
故答案为:2015.
点评 本题考查算法的多样性,正确理解秦九韶算法求多项式的原理是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
14.函数y=log(x-2)(5-x)的定义域是( )
| A. | (3,4) | B. | (2,5) | C. | (2,3)∪(3,5) | D. | (-∞,2)∪(5,+∞) |
1.已知α,β为锐角△ABC的两个内角,x∈R,f(x)=($\frac{cosα}{sinβ}$)|x-2|+($\frac{cosβ}{sinα}$)|x-2|,则关于x的不等式f(2x-1)-f(x+1)>0的解集为( )
| A. | (-∞,$\frac{4}{3}$)∪(2,+∞) | B. | ($\frac{4}{3}$,2) | C. | (-∞,-$\frac{4}{3}$)∪(2,+∞) | D. | (-$\frac{4}{3}$,2) |
11.下列结论中,正确的是( )
| A. | “x>2”是“x2-2x>0”成立的必要条件 | |
| B. | 命题“若x2=1,则x=1”的逆否命题为假命题 | |
| C. | 命题“p:?x∈R,x2≥0”的否定形式为“¬p:?x0∈R,x02≥0” | |
| D. | .已知向量$\overrightarrow a,\overrightarrow b$,则“$\overrightarrow a∥\overrightarrow b$”是“$\overrightarrow a+\overrightarrow b=\overrightarrow 0$”的充要条件 |
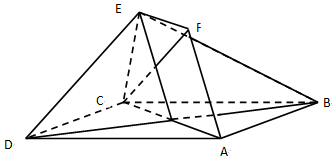 (文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.