题目内容
已知椭圆C: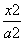 +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:(x-3)2+(y-1)2=3相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:(x-3)2+(y-1)2=3相切.
(1)求椭圆C的方程;
(2)若不过点A的动直线l与椭圆C交于P、Q两点,且 =0.求证:直线l过定点,并求出该定点的坐
=0.求证:直线l过定点,并求出该定点的坐 标.
标.
1)椭圆的方程为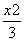 +y2=1.
+y2=1.
(2)由 ·
·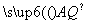 =0知AP⊥AQ,从而直线AP与坐标轴不垂直,故可设直线AP的方程为y=kx+1,直线AQ的方程为y=-
=0知AP⊥AQ,从而直线AP与坐标轴不垂直,故可设直线AP的方程为y=kx+1,直线AQ的方程为y=-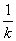 x+1,
x+1,
将y=kx+1代入椭圆C的方程,
整理得(1+3k2)x2+6kx=0,
 所以直线l过定点(0,-
所以直线l过定点(0,- ).
).

练习册系列答案
相关题目
cos 390°=( )
390°=( )
|
| A. |
| B. |
| C. |
| D. | ﹣ |
 的实数根
的实数根 叫做函数
叫做函数 的“新驻点”,若函数
的“新驻点”,若函数 ,
, ,
, 的“新驻点”分别为
的“新驻点”分别为 ,则
,则 B.
B. C.
C. D.
D.
 的参数方程是
的参数方程是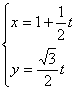 (
(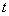 为参数),以原点
为参数),以原点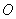 为极点,
为极点,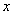 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆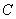 的极坐标方程为
的极坐标方程为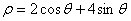 ,则直线
,则直线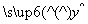 =3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
=3+2x,当变量x增加2个单位,其预报值平均增加4个单位;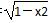 x”是“函数y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
x”是“函数y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件; 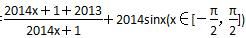 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是________个.
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是________个. 是等差数列
是等差数列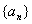 的前n项和,若
的前n项和,若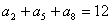 , 则
, 则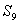 等于( )
等于( )

