题目内容
8.已知函数f(x)=x(ex-e-x),若f(a+3)>f(2a),则a的范围是-1<a<3.分析 求出函数f(x)的奇偶性,求出函数的单调性,问题转化为|a+3|>|2a|,求出a的范围即可.
解答 解:函数f(x)=x(ex-e-x)=f(-x),
函数f(x)=x(ex-e-x)是偶函数,
而f′(x)=(ex-e-x)+x(ex+e-x),
x>0时,f′(x)>0,f(x)递增,
故x<0时,f(x)递减,
∵f(a+3)>f(2a),
∴|a+3|>|2a|,
解得:-1<a<3,
故答案为:-1<a<3.
点评 本题考查了求函数的奇偶性、单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
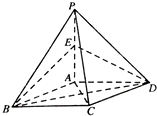 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°. 如图,已知AB是圆O的直径,直线CD与圆O相切于点C,弦AE的延长线交CD于点D,若∠DAC=∠CAB.
如图,已知AB是圆O的直径,直线CD与圆O相切于点C,弦AE的延长线交CD于点D,若∠DAC=∠CAB.