题目内容
16.若正数a,b满足ab=a+b+3.(1)求ab的取值范围.
(2)求a+b的取值范围.
分析 (1)正数a,b满足ab=a+b+3,可得ab=a+b+3≥$2\sqrt{ab}$+3,解出即可得出.
(2)正数a,b满足ab=a+b+3,可得a+b+3=ab≤$(\frac{a+b}{2})^{2}$,解出即可得出.
解答 解:(1)∵正数a,b满足ab=a+b+3,
∴ab=a+b+3≥$2\sqrt{ab}$+3,即$(\sqrt{ab})^{2}$-2$\sqrt{ab}$-3≥0,
解得$\sqrt{ab}$≥3,即ab≥9,当且仅当a=b=3时取等号,∴ab∈[9,+∞).
(2)∵正数a,b满足ab=a+b+3,∴a+b+3=ab≤$(\frac{a+b}{2})^{2}$,
即(a+b)2-4(a+b)-12≥0,解得a+b≥6,当且仅当a=b=3时取等号,
∴a+b∈[6,+∞).
点评 本题考查了基本不等式的性质、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.口袋中放有大小相等的2个红球和1个白球,有放回地每次摸取1个球,定义数列{an}:若第n次摸到红球,an=-1;若第n次摸到白球,an=1.如果Sn为数列{an}的前n项和,那么S7=3的概率为( )
| A. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | B. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{1}{3}})^5}$ | C. | $C_7^3×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | D. | $C_7^2×{({\frac{2}{3}})^2}×{({\frac{1}{3}})^5}$ |
5. 一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
 一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )| A. | π+1 | B. | π+2 | C. | 2π+1 | D. | $3π+5+2\sqrt{2}$ |
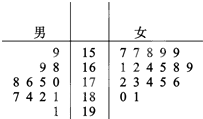 某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm
某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm