题目内容
18.已知f(x)为奇函数,当x<0时,f(x)=x+ln(-x),则曲线y=f(x)在点(e,f(e))处的切线方程为y=(1-$\frac{1}{e}$)x.分析 求出当x>0时,-y=-x+lnx,y=x-lnx,求出导函数,可得切线斜率,利用点斜式可得切线方程.
解答 解:当x>0时,-y=-x+lnx,y=x-lnx,y′=1-$\frac{1}{x}$,
切线方程为y-(e-1)=(1-$\frac{1}{e}$)(x-e),即y=(1-$\frac{1}{e}$)x.
故答案为y=(1-$\frac{1}{e}$)x.
点评 本题考查奇函数的性质,考查导数的几何意义,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知集合A={a-2,2a2+5a,12},-3∈A,则a的值为( )
| A. | -1 | B. | $-\frac{3}{2}$ | C. | $-1或-\frac{3}{2}$ | D. | $-1或-\frac{3}{2}$ |
3.某几何体的三视图如图所示,则此几何体的外接球表面积等于( )
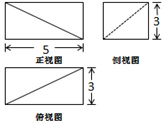

| A. | $\frac{75π}{2}$ | B. | 30π | C. | 43π | D. | 15π |
7.已知椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2为其左、右焦点,A,B分别为其左、右顶点,若4$\overrightarrow{A{F_1}}$=$\overrightarrow{{F_1}B}$,则该椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
8.已知函数f(x)=log2x,x∈(4,8),则函数y=f(x2)+$\frac{8}{f(x)}$的值域为( )
| A. | [8,10) | B. | ($\frac{26}{3}$,10) | C. | (8,$\frac{26}{3}$) | D. | ($\frac{25}{3}$,10) |