题目内容
17.设集合P满足{1,2}⊆P⊆{0,1,2,3,4},满足条件的P的个数为8.分析 由子集性质利用列举法列举出满足条件的所有的集体合P,由此能求出结果.
解答 解:∵集合P满足{1,2}⊆{0,1,2,3,4},
∴满足条件的P有:
{1,2},{1,2,0},{1,2,3},{1,2,4},{1,2,0,3},
{1,2,0,4},{1,2,3,4},{0,1,2,3,4},
共有8个.
故答案为:8.
点评 本题考查满足条件集合个数的求法,是基础题,解题时要认真审题,注意子集定义的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知函数$f(x)={2016^x}+{log_{2016}}(\sqrt{{x^2}+1}+x)-{2016^{-x}}$+2,则关于x的不等式f(3x+1)+f(x)>4的解集为( )
| A. | (-$\frac{1}{2016}$,+∞) | B. | (-$\frac{1}{3}$,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | (-$\frac{1}{4}$,+∞) |
8.在△ABC中,BC=7,cosA=$\frac{1}{5}$,sinC=$\frac{2\sqrt{6}}{7}$,若动点P满足$\overrightarrow{AP}$=2$λ\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$(λ∈R),则点P的轨迹与直线AB,AC所围成的封闭区域的面积为( )
| A. | 3$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 6$\sqrt{6}$ | D. | 12$\sqrt{6}$ |
9.甲、乙、丙、丁四人参加国际奥林匹克数学竞赛选拔赛,四人的平均成绩和方差如表:
从这四人中选择一人参加国际奥林匹克数学竞赛,最佳人选是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均成绩$\overline x$ | 89 | 89 | 86 | 85 |
| 方差S2 | 2.1 | 3.5 | 2.1 | 5.6 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
6.非空集A={x|2a+1≤x≤3a-5},B=$\{x|y=\sqrt{(3-x)(x-22)}\}$,则A⊆A∩B的一个充分不必要条件是( )
| A. | 1≤a≤9 | B. | 6<a<9 | C. | 6≤a≤9 | D. | a≤9 |
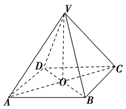 如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.