Question

8．在△ABC中，BC=7，cosA=$\frac{1}{5}$，sinC=$\frac{2\sqrt{6}}{7}$，若动点P满足$\overrightarrow{AP}$=2$λ\overrightarrow{AB}$+（1-λ）$\overrightarrow{AC}$（λ∈R），则点P的轨迹与直线AB，AC所围成的封闭区域的面积为（　　）

• A． 3$\sqrt{6}$
• B． 4$\sqrt{6}$
• C． 6$\sqrt{6}$
• D． 12$\sqrt{6}$

Answer 1

分析 根据向量加法的几何意义得出P点轨迹，利用正弦定理解出AB，得出△ABC的面积，从而求出围成封闭区域的面积，从而求出围成封闭区域的面积．

解答 解：延长AB至D，使得AD=2AB，连结CD，则
∵$\overrightarrow{AP}$=2$λ\overrightarrow{AB}$+（1-λ）$\overrightarrow{AC}$=λ$\overrightarrow{AD}$+（1-λ）$\overrightarrow{AC}$．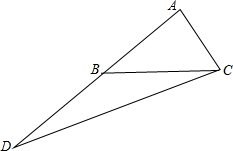
∴C，D，P三点共线．
∴P点轨迹为直线CD．
在△ABC中，sinA=$\frac{2\sqrt{6}}{5}$．sinC=$\frac{5}{7}$．
由正弦定理得AB=5．
sinB=sin（A+C）=sinAcosC+cosAsinC=$\frac{12\sqrt{6}}{35}$
∴S_△ABC=$\frac{1}{2}×5×7×\frac{12\sqrt{6}}{35}$=6$\sqrt{6}$
∴S_△ACD=2S_△ABC=12$\sqrt{6}$．
故选：D．

点评 本题考查了平面向量线性运算的几何意义，考查学生的计算能力，确定P点轨迹是关键，属于中档题．