题目内容
12. 设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).(1)如图是用“五点法”画函数f(x)简图的列表,试根据表中数据求出函数f(x)的表达式;
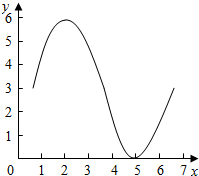
(2)填写表中空格数据,并根据列表在所给的直角坐标系中,画出函数f(x)在一个周期内的简图.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2 | 5 | |||
| y | 6 | 0 |
分析 (1)根据五点法对应的数据关系求出相应的参数.
(2)根据函数的解析式即可得到结论
解答 解:(1)由表格可知,Asin$\frac{π}{2}$+B=A+B=6,Asin$\frac{3π}{2}$+B=-A+B=0,
解得A=3,B=3,
且2ω+φ=$\frac{π}{2}$,5ω+φ=$\frac{3π}{2}$,解得ω=$\frac{π}{3}$,φ=-$\frac{π}{6}$.
则f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)+3,
(2)由表格数据可得:
| $\frac{π}{3}$x-$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{1}{2}$ | 2 | $\frac{7}{2}$ | 5 | $\frac{13}{2}$ |
| y | 3 | 6 | 3 | 0 | 3 |
点评 本题主要考查三角函数的图象,根据五点法对应的数据关系求出相应的参数时解决本题的关键.

练习册系列答案
相关题目
20.下列关系不正确的是( )
| A. | a>b⇒a+c>b+c | B. | a>b,c>0⇒ac>bc | ||
| C. | a>b⇒a2>b2 | D. | a>b且c>d⇒a+c>b+d |
4.已知直线x+my+6=0和(m-2)x+3y+2m=0互相平行,则实数m的取值为( )
| A. | -1或3 | B. | -1 | C. | -3 | D. | 1或-3 |