题目内容
15.设数列{an}的前n项和为Sn,Sn=$\frac{{a}_{1}({3}^{n}-1)}{2}$(对n≥1恒成立)且a4=54,则an=$\frac{2}{3}•{3}^{n}$.分析 先求出a4=S4-S3=27a1=54,从而得到Sn=$\frac{{a}_{1}({3}^{n}-1)}{2}$=3n-1,由此能求出an.
解答 解:∵数列{an}的前n项和为Sn,Sn=$\frac{{a}_{1}({3}^{n}-1)}{2}$(对n≥1恒成立),且a4=54,
∴a4=S4-S3=$\frac{{a}_{1}(81-1)}{2}-\frac{{a}_{1}(27-1)}{2}$=27a1,
∵a4=54,∴a1=2,
∴Sn=$\frac{{a}_{1}({3}^{n}-1)}{2}$=3n-1,
∴an=Sn-Sn-1=(3n-1)-(3n-1-1)=$\frac{2}{3}•{3}^{n}$.
n=1时,上式成立,∴an=$\frac{2}{3}•{3}^{n}$.
故答案为:$\frac{2}{3}•{3}^{n}$.
点评 本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意公式an=Sn-Sn-1的合理运用.
Sn=$\frac{{a}_{1}(3n-1)}{2}$更正为:Sn=$\frac{{a}_{1}({3}^{n}-1)}{2}$.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
10.已知全集U=R,集合A=$\left\{{x|y=\frac{1}{lnx}}\right\}$,B=$\left\{{x|y=\sqrt{-{x^2}+x}}\right\}$,则(∁UA)∩B=( )
| A. | {0} | B. | {0,1} | C. | ∅ | D. | (0,1) |
7.已知P为直线y=kx+b上一动点,若点P与原点均在直线x-y+2=0的同侧,则k,b满足的条件分别为( )
| A. | k=1,b<2 | B. | k=1,b>2 | C. | k≠1,b<2 | D. | k≠1,b>2 |
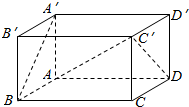 如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.
如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.