题目内容

5．若函数y=f（x）的定义域是[1，9]，则函数y=f（3x）的定义域为[0，2]．

分析 利用函数的定义域，列出不等式求解即可．

解答 解：若函数y=f（x）的定义域是[1，9]，
则1≤3x≤9，
则30≤3x≤32，
故0≤x≤2，
故答案为：[0，2]．

点评 本题考查函数的定义域的求法，是基础题．

练习册系列答案
相关题目
15．在空间直角坐标系中，A，B，C三点到坐标分别为A（2，1，-1），B（3，4，λ），C（2，7，1），若$\overrightarrow{AB}⊥\overrightarrow{CB}$，则λ=（　　）
A．3B．1C．±3D．-3
16．已知函数f（x）定义域为R，若存在常数f（x），使$|f（x）|≤\frac{k}{2017}|x|$对所有实数都成立，则称函数f（x）为“期望函数”，给出下列函数：
①f（x）=x2②f（x）=xex③$f（x）=\frac{x}{{{x^2}-x+1}}$④$f（x）=\frac{x}{{{e^x}+1}}$
其中函数f（x）为“期望函数”的是③④．（写出所有正确选项的序号）
13．设实数x，y满足约束条件$\left\{\begin{array}{l}2x+y-6≥0\\ x+2y-6≤0\\ y≥0\end{array}\right.$，则$\frac{{2{y^2}-xy}}{x^2}$的最小值是（　　）
A．$-\frac{1}{8}$B．$\frac{1}{8}$C．0D．1
20．已知全集U={0，1，3，4，5，6，8}，集合A={1，4，5，8}，B={2，6}，则集合（∁UA）∪B=（　　）
A．{1，2，5，8}B．{0，3，6}C．{0，2，3，6}D．∅
10．已知函数$f（x）=\frac{{a{x^2}+4}}{x}$，且f（1）=5．
（1）求a的值；
（2）判断f（x）的奇偶性，并加以证明；
（3）判断函数f（x）在[3，+∞）上的单调性，并加以证明．
17．男队有号码1，2，3的三名乒乓球运动员，女队有号码为1，2，3，4的四名乒乓球运动员，现两队各出一名运动员比赛一场，则出场的两名运动员号码不同的概率为$\frac{3}{4}$．
14．若直线l1：（k-3）x+（k+4）y+1=0与l2：（k+1）x+2（k-3）y+3=0垂直，则实数k的值是（　　）
A．3或-3B．3或4C．-3或-1D．-1或4
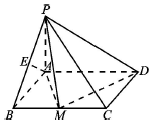15．如图，四棱锥P-ABCD，底面ABCD为矩形，AB=PA=$\sqrt{3}$，AD=2，PB=$\sqrt{6}$，E为PB中点，且AE⊥PC．
（1）求证：PA⊥平面ABCD；
（2）线段BC上是否存在点M使得二面角P-MD-A的大小为60°？若存在，求出BM的长，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网