题目内容
13．设实数x，y满足约束条件$\left\{\begin{array}{l}2x+y-6≥0\\ x+2y-6≤0\\ y≥0\end{array}\right.$，则$\frac{{2{y^2}-xy}}{x^2}$的最小值是（ ）| A． | $-\frac{1}{8}$ | B． | $\frac{1}{8}$ | C． | 0 | D． | 1 |
分析 作出不等式组对应的平面区域，$\frac{{2{y^2}-xy}}{x^2}$=2$（\frac{y}{x}）^{2}-\frac{y}{x}$，最利用k=$\frac{y}{x}$的几何意义，结合直线斜率公式进行求解即可
解答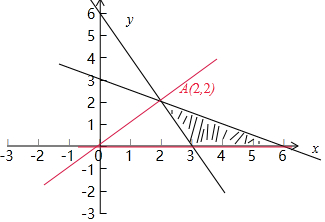 
解：作出不等式组对应的平面区域，k=$\frac{y}{x}$的几何意义为区域内的点到原点的斜率，
由图象可知，OA的斜率最大，由$\left\{\begin{array}{l}{2x+y-6=0}\\{x+2y-6=0}\end{array}\right.$得A（2，2），
∴0≤k≤1，∴$\frac{{2{y^2}-xy}}{x^2}$=2$（\frac{y}{x}）^{2}-\frac{y}{x}$=2k2-k=2（k-$\frac{1}{4}$）2-$\frac{1}{8}$$≥-\frac{1}{8}$，
故选：A．
点评 本题考查简单线性规划，涉及直线的斜率公式，准确作图是解决问题的关键，属中档题
练习册系列答案
名校课堂系列答案
相关题目
3．设函数f（x）=ex（sinx-cosx）（0≤x≤4π），则函数f（x）的所有极大值之和为（ ）
| A． | e4π | B． | eπ+e2π | C． | eπ-e3π | D． | eπ+e3π |
1．某种商品价格与该商品日需求量之间的几组对照数据如表：
（1）求y关于x的线性回归方程；
（2）利用（1）中的回归方程，当价格x=40元/kg时，日需求量y的预测值为多少？
参考公式：线性回归方程$y=bx+\hat a$，其中$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（x_i^{\;}-\overline x）}^2}}}}，\hat a=\overline y-\hat b\overline x$．
| 价格x（元/kg） | 10 | 15 | 20 | 25 | 30 |
| 日需求量y（kg） | 11 | 10 | 8 | 6 | 5 |
（2）利用（1）中的回归方程，当价格x=40元/kg时，日需求量y的预测值为多少？
参考公式：线性回归方程$y=bx+\hat a$，其中$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（x_i^{\;}-\overline x）}^2}}}}，\hat a=\overline y-\hat b\overline x$．
8．已知$cosα-sinα=\frac{1}{2}$，则sinαcosα等于（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{3}{2}$ |