题目内容
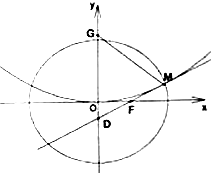 已知椭圆K 1:
已知椭圆K 1:| x2 |
| a2 |
| y2 |
| b2 |
(1)若点M(2,1),求c;
(2)求a、c、p的关系式;
(2)试问△MDG能否为正三角形?若能请求出椭圆的离心率,若不能请说明理由.
考点:圆锥曲线的综合,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)代入点M(2,1)确定抛物线方程,求出点M处的切线,即可求出c;
(2)设出点M的坐标,表示出切线方程,将y=0代入,即可得出c,再将点M的坐标代入椭圆方程即可得出a、c、p的关系式;
(3)假设△MDG能为正三角形,从确定MD的斜率,得出p和c的关系,在代入(2)中的关系,得出a和c的关系式,同除a4即可得到关于e的方程.
(2)设出点M的坐标,表示出切线方程,将y=0代入,即可得出c,再将点M的坐标代入椭圆方程即可得出a、c、p的关系式;
(3)假设△MDG能为正三角形,从确定MD的斜率,得出p和c的关系,在代入(2)中的关系,得出a和c的关系式,同除a4即可得到关于e的方程.
解答:
解:(1)当M点的坐标为(2,1)时,
抛物线方程为x2=4y,
即y=
.
其在点(2,1)M处切线方程为
y-1=x-2.
与x轴的交点为(1,0),
∴c=1.
(2)设M点的坐标为(x0,
),(x0>0)
∵y=
x2,
∴y′=
.
∴切线l:y-
=
(x-x0),
即:y=
x-
.
令x=0得,D(0,
).
∵切线l过右焦点F,
则x0=2c,
∴y0=
=
.
∵点M在椭圆上,
∴
+
=1.
(3)∵点G为抛物线的焦点,
∴MG=y0+
=
+
,
GD=yG-yD=
+
,
∴GD=MG,
即△MDG为等腰三角形,
若△MDG为等边三角形,
则直线MD的倾斜角为30°,
即直线MD的斜率为
,
∴
=
,
∴p=2
c,
代入
+
=1得,
12c4-16a2c2+3a4=0,
同除a4得,12e4-16e2+3=0,
解得,e2=
=
=
或e2=
>1(舍去)
∴e=
=
.
综上,若△MDG能为正三角形,此时椭圆的离心率为
.
抛物线方程为x2=4y,
即y=
| x2 |
| 4 |
其在点(2,1)M处切线方程为
y-1=x-2.
与x轴的交点为(1,0),
∴c=1.
(2)设M点的坐标为(x0,
| x02 |
| 2p |
∵y=
| 1 |
| 2p |
∴y′=
| x |
| p |
∴切线l:y-
| x02 |
| 2p |
| x0 |
| p |
即:y=
| x0 |
| p |
| x02 |
| 2p |
令x=0得,D(0,
| x02 |
| 2p |
∵切线l过右焦点F,
则x0=2c,
∴y0=
| x02 |
| 2p |
| 2c2 |
| p |
∵点M在椭圆上,
∴
| 4c2 |
| a2 |
| 4c4 |
| (a2-c2)p2 |
(3)∵点G为抛物线的焦点,
∴MG=y0+
| p |
| 2 |
| x02 |
| 2p |
| p |
| 2 |
GD=yG-yD=
| p |
| 2 |
| x02 |
| 2p |
∴GD=MG,
即△MDG为等腰三角形,
若△MDG为等边三角形,
则直线MD的倾斜角为30°,
即直线MD的斜率为
| ||
| 3 |
∴
| 2c |
| p |
| ||
| 3 |
∴p=2
| 3 |
代入
| 4c2 |
| a2 |
| 4c2 |
| (a2-c2)p2 |
12c4-16a2c2+3a4=0,
同除a4得,12e4-16e2+3=0,
解得,e2=
4-
| ||
| 6 |
7-2
| ||
| 12 |
(
| ||
| 12 |
或e2=
4+
| ||
| 6 |
∴e=
| ||
2
|
| ||||
| 6 |
综上,若△MDG能为正三角形,此时椭圆的离心率为
| ||||
| 6 |
点评:本题主要考查抛物线的标准方程和简单几何性质,椭圆的标准方程和简单几何性质的应用,以及利用齐次式求离心率的方法,属于难题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目